关于【假设检验的步骤和原理】，今天犇涌小编给您分享一下，如果对您有所帮助别忘了关注本站哦。

1、假设检验的步骤和原理：一文读懂统计学中的“假设检验”到底是什么？

今天给大家讲一篇关于统计学的知识，虽然当前机器学习，深度学习等大数据技术火得一塌糊涂，但归根结底，离不开统计学的基础，而谈到统计学，假设检验几乎是提到的最多的词语，到底什么是假设检验， 什么是P值，什么时候用t检验，什么时候用F检验，非统计学背景的同学可能一脸懵逼，接下来我就讲下什么是假设检验

什么是假设检验？

首先明确下假设检验在统计学里的地位：统计推断是统计学的重要分支，做统计推断有两个重要方法，即参数估计与假设检验。参数估计是用样本统计量估计总体参数，简单来说就是样本表现啥样，我就推断总体是啥样。而假设检验，则顾名思义，先提出一个假设，然后检验假设是否靠得住，例如假设均值为μ，然后根据样本信息检验均值是不是μ，通常我们是要去证明均值不是μ，也就是去推翻原假设。逻辑上采用的是反证法，根据统计上的小概率原理，即假设是这样，但样本表现却不是这样，从而否定原假设。

举例来说，某官方数据说居民人均收入10000，但我觉得这个不对，于是就局部范围内做了个统计（假如样本有代表性），统计出来平均值为7000, 那我这个结果有没有信服力，那我们可以检验一下，计算出P值为0.0002，那我可以很自信地说官方数据不对，不值得信。因为P值为0.0002意味着，如果居民人均工资为1w， 那么我统计出均值为7k的概率为0.0002，这么小的概率竟然这么容易就让我选的这个局部统计碰上了，显然真实的人均工资不可能为1w啊， 这就是根据小概率原理来推翻原假设。

假设检验的基本步骤

接下来我们讲一下假设检验的步骤，讲述过程中你也许会有疑问，为什么这样，不要担心，先往下看，我会陆续对假设检验的细节作出补充，如果未涉及到可以在评论中提出，我会补充上）：

步骤1，提出假设，也就是我猜结果会是什么。猜完之后进入步骤2，即我要拿什么去验证假设，这里我们叫做检验统计量。检验没有绝对的对错，所以我们要设定一个显著性水平，就是步骤3，相当于设定一个门槛，在门外面就拒绝进门，统计学上叫拒绝域，拒绝的是原假设。套路第四步就是将门在哪儿计算出来，依据的是前两步确定的检验统计量以及显著性水平。最后就可以做出决策啦，看一下到底在门里面还是门外面。

接下来将提到的步骤跟大家详细说一下：

假设的提出包括原假设与备择假设。原假设（H0）则是我们收集证据想要推翻的假设, 而备择假设（H1）则是要去支持的，所以大家可以根据实际情况来设定原假设与备择假设。原假设与备择假设互斥。假设检验是围绕着对原假设是否成立展开的。假设检验还会涉及到两类错误的问题，这个内容较多，会单独讲解。

检验统计量是用于假设检验决策的统计量。如何去选择统计量呢？这与参数估计相同，需要考虑样本总体个数，样本大小，通常大于30个样品我们认为是大样本，以及总体方差是否已知，如果未知，可以用样品方差近似计算。是不是感觉有些头晕，撑住，这是做假设检验的关键，告诉你什么情况下采用什么样的检验方法，记住这儿，以后就不会没心没肺的只会t检验啦。贴心的我给大家整理了检验统计量的选择图谱，对家直接对号入座就可以啦，记住这些，再遇到假设检验的问题，你会感觉厉（niu）害(bi)的不要不要的。

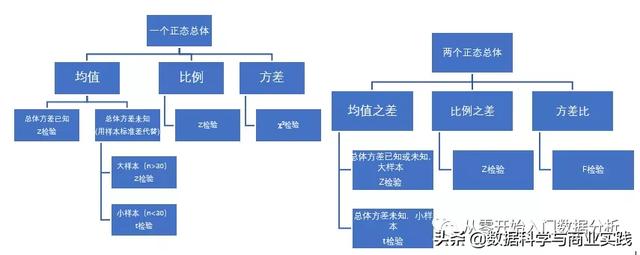
配对样本的检验：两个总体参数的假设检验过程中，我们假定样本是独立的，但有种情况下样本间可能存在相依的关系，这种情况下两个正态总体的问题可以按照一个样品总体进行分析。举个例子：我想测试某个洗涤产品的洗涤效果，我可以测一下衣服洗之前的洁净程度，用产品洗之后的洁净程度，这样就得到了两个总体，可以按照方差未知的小样本t检验进行分析。但是，同是一件衣服，洗之前和洗之后数据之间是有对应关系的，我可以将洗前洗后的洁净程度做差值，检验差值是否为0，这样就转化为一个总体样本的t检验。

具体的统计量的计算公式此处未给出，主要考虑到现在都用统计软件进行计算，关键要明确自己的统计问题，选择恰当的检验统计量，然后在统计软件上就可以开挂了！

显著性α：这是犯一类错误的概率，即原假设为真时，拒绝原假设的概率。比如警察抓小偷时，明明是小偷，却判断失误当好人给放了的概率。也被称为抽样分布的拒绝域，这个可以由研究者事先确定。

计算检验统计量的值。当确定了检验统计量以及显著性α的值，通常为0.01, 0.05，0.001，就可以通过统计软件或查表得到统计量的临界值za或za/2，ta或ta/2

作出统计决策。统计决策的确定有两种方式，一种是将检验统计量的绝对值与α水平的临界值进行比较，高于临界值则拒绝原假设，低于临界值则不能拒绝。另外一种方式是采用P值进行决策。个人比较倾向第二种，当然现在的统计学软件会将这些值一并给出。我们通常将P值称为观测到的显著性水平，即当原假设为真时得到样本观察结果或者更极端结果的概率，如果P值很小，说明得到观测结果的概率很小，如果出现了，根据小概率原理，我就有理由拒绝原假设了。如果事先确定了显著性水平，比如α= 0.05，在双侧检验中可以比较P值与0.025的大小决定是否拒绝原假设，单侧检验中可以比较P值与0.05的大小进行决策。当然也可以直接使用P值，按照我们所需要的显著性水平进行决策。

双侧检验

单侧检验

以上就是假设检验的基本原理及流程。懂了这些就几乎可以秒杀一切你所遇到的假设检验问题。还有同学经常问为何把小概率标准定为0.05， 哈哈，不要问我，因为我不知道。著名英国统计学家Fisher就这样用的，无解。

举例说明：

“多吃谷物，将有助于减肥。”为了验证这个假设，随机抽取了35人，询问他们早餐和午餐的通常食谱，根据他们的食谱，将其分为二类，一类为经常的谷类食用者(总体1)，一类为非经常谷类食用者(总体2)。然后测度每人午餐的大卡摄取量。经过一段时间的实验，得到如下结果：检验该假设(a = 0.05)

1. 原假设：u1-u2>=0

备择假设：u1-u2<0

2. 该情况为两个总体的t检验, 计算得t=2.4869。注意此处为单侧检验。

3. 在0.05显著性水平上拒绝原假设。

4. 结论，没有证据证明多次谷物有助于减肥。

2、假设检验的步骤和原理，一篇搞懂假设检验

一、常用核心概念

什么是假设检验：假设就是对从总体参数(均值、比例等)的具体数值所作的陈述，比如，我认为配方一比配方二的效果要好。而假设检验就是先对总体的参数提出某种假设，然后利用样本的信息判断假设是否成立的过程，比如上面的假设信息我该接受还是拒绝。

什么是显著性水平：显著性水平是一个概率值，原假设为真时，拒绝原假设的概率，表示为α，常取值为0.05、0.01、0.10。一个公司招聘，本来准备招聘100个人，公司希望只有5%的人是混水摸鱼招聘进来，所以可能会有5个人混进来，所谓显著性水平α，就是你允许有多少比例混水摸鱼的能通过测试。

原假设与备择假设：待检验的假设又叫原假设(零假设)，一般表示为H0，原假设一般表示两者没有显著性差异。与原假设进行对比的叫备择假设，表示为H1。一般在比较的时候，主要有等于、大于、小于。

检验统计量：即计算检验的统计量。根据给定的显著性水平，查表得出相应的临界值。再将检验统计量的值与该显著性水平的临界值进行比较，得出是否拒绝原假设的结论。

P值：是一个概率值，如果原假设为真，p值是抽样分布中大于或小于样本统计量的概率。左检验时，p值为曲线上方小于等于检验统计量部分的面积。右检验时，p值为曲线上方大于等于检验统计量部分的面积。

假设检验的两种错误：类型 I 错误(弃真)，如原假设为真，但否定它，则会犯类型 I 错误。犯类型 I 错误的概率为 α（即您为假设检验设置的显著性水平）。α 为 0.05 表明，当您否定原假设时，您愿意接受 5% 的犯错概率。为了降低此风险，必须使用较低的 α 值。但是，使用的α值越小，在差值确实存在时检测到实际差值的可能性也越小。类型 II 错误(采伪)，如原假设为假，但无法否定它，则会犯类型 II 错误。犯类型 II 错误的概率为 β，β 依赖检验功效。可以通过确保检验具有足够大的功效来降低犯类型 II 错误所带来的风险。方法是确保样本数量足够大，以便在差值确实存在时检测到实际差值。

单双测检验：当假设关键词有不得少于/低于的时候用左侧检验，比如灯泡的使用寿命不得少于/低于700小时时；当假设关键词有不得多于/高于的时候用右侧检验，比如次品率不得多于/高于5%时。双侧检验指按分布两端计算显著性水平概率的检验，应用于理论上不能确定两个总体一个一定比另一个大或小的假设检验。一般假设检验写作H0：μ1=μ2。

检验结果：单侧，若p值>α,不拒绝H0，若p值<α,拒绝H0；双侧，若p值>1/2α,不拒绝H0，若p值<1/2α,拒绝H0

二、假设检验方法

假设检验方法：z检验，t检验，卡方检验(卡方本篇不详述，应用较少)

2.1 Z检验

Z检验原理：当总体标准差已知,样本量较大时用标准正态分布的理论来推断差异发生的概率，从而比较两个平均数的差异是否显著。如果检验一个样本平均数与一个已知的总体平均数的差异是否显著，其Z值计算公式为：

如果检验来自两个的两组样本平均数的差异性，从而判断它们各自代表的总体的差异是否显著，其Z值计算公式为：

Z检验实例：

研究正常人与高血压患者胆固醇含量，比较两组血清胆固醇含量有无显著差异。

正常人组数据:n1=506(样本量) μ1=180.6(样本均值) s1=34.2(标准差)

高血压组数据:n2=142 μ2=223.6 s2=45.8

1、提出假设，规定适当检验统计量，确定检验水平：

H0：μ1=μ2

H1：μ1≠μ2

α=0.05，样本量较大，且检验来自两组样本平均数的差异性，故选择z检验统计量

2、计算统计量z值

将已知数据带入z检验公式，

计算假设检验统计量 z=10.4

α=0.05，双侧故 α/2=0.025，1-α=0.975 查表，确认临界值为1.96

3、确定p值，做出推断结论

10.4(z值)>1.96(临界值)，故p<0.05，按α=0.05水准拒绝H0，接受H1，可以认为正常人和高血压患者的血清胆固醇含量有差异。

2.2 t检验

t检验：分为单样本的t检验、配对样本均数t检验(本篇不详细说)、两独立样本均数t检验。t检验应用于两组计量资料小样本比较，样本对总体有较好代表性，对比组间有较好组间均衡性，即随机抽样和随机分组。且样本来自正态分布总体。单个样本t检验适用于样本均数与已知总体均数μ0的比较,目的是检验样本均数所代表的总体均数μ是否与已知总体均数μ0有差别。应用于总体标准α未知的小样本资料,且服从正态分布。

单样本t检验实例：

某地新生儿出生体重为3.3kg，从该地难产儿中随机抽取35名婴儿，平均体重为3.42kg，标准差为0.4kg，问该地难产儿出生体重与新生儿体重是否不同？

1、提出假设，规定适当检验统计量，确定检验水平：

H0：μ=μ0

H1：μ≠μ0

α=0.05 ，样本均数与已知总体均数μ0的比较，所以选择单样本t检验

2、计算统计量z值

n=35 μ0=3.3 μ=3.42 s=0.4

自由度=n-1=34，α=0.05，双侧故 α/2=0.025，1-α=0.975，自由度34，查表得出临界值为2.032

3、确定p值，做出推断结论

因为1.77(z值)<2.032(临界值)，故p>0.05，按α=0.05水平，差别无统计学意义，不拒绝h0，不能认为该地难产儿与新生儿体重有差异。

两独立样本t检验(ab实验背后原理)：适用于完全随机设计的两样本均数的比较,其目的是检验两样本所来自总体的均数是否相等。两独立样本t检验要求两样本所代表的总体服从正态分布N(μ1，σ^2)和N(μ2，σ^2)，且两总体方差σ1^2、σ2^2相等,即方差齐性。若两总体方差不等需要先进行变换。两独立样本t检验的检验假设是两总体均数相等,即H0：μ1=μ2，统计量计算公式为：

两独立样本t检验实例：

25例糖尿病患者随机分成两组，甲单纯药物治疗，乙采用药物合并饮食治疗，二月后测空腹血糖如下，问两种疗法血糖值是否相同？

数据：n1=12 s1=182.5 n2=13 s2=141

1、提出假设，规定适当检验统计量，确定检验水平：

H0：μ1=μ2 H1：μ1≠μ2

α=0.05, 选用两独立样本t检验方法

2、计算统计量z值

将数据带入公式，计算得t=2.639

自由度=n1 n2-2=23 α=0.05，双侧故 α/2=0.025，1-α=0.975，查表得临界值为 t=2.069

3、确定p值，做出推断结论

因为2.639(t值)>2.069(临界值) ，故 p<0.05 ， 在0.05水准下，拒绝H0，接受H1，存在显著性差异，故认为两种疗法效果不同。

作者：赵小洛 一线互联网公司数据分析师、商业分析师，主刊互联网数据分析相关、方法论、复盘、思考总结。

本文关键词：假设检验的一般步骤包括哪些，假设检验的具体步骤，假设检验的步骤及原理，假设检验的步骤和原理，假设检验的基本原理和步骤。这就是关于《假设检验的步骤和原理，一文读懂统计学中的“假设检验”到底是什么》的所有内容，希望对您能有所帮助！更多的知识请继续关注《犇涌向乾》百科知识网站：！