1、红黑树的简介

红黑树（Red Black Tree） 是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构。

红黑树是在1972年由Rudolf Bayer发明的，当时被称为平衡二叉B树（symmetric binary B-trees）。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。 

红黑树是一种特化的AVL树（平衡二叉树），都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。 

它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的： 它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目

2、红黑树的优点

• 红黑树保证了一种弱平衡，即树的高度最多是2倍的对数级别。这使得红黑树在插入和删除操作时具有更高的灵活性
• AVL树是一种严格的平衡树，保证任何节点的左子树和右子树的高度差（平衡因子）不超过1。这确保了AVL树在平衡方面表现更好，但在插入和删除操作时可能需要更多的旋转来维持平衡
• 红黑树是具备了某些特性的二叉搜索树，能解决非平衡树问题，红黑树是一种接近平衡的二叉树（说它是接近平衡因为它并没有像AVL树的平衡因子的概念，它只是靠着满足红黑节点的5条性质来维持一种接近平衡的结构，进而提升整体的性能，并没有严格的卡定某个平衡因子来维持绝对平衡）

3、红黑树的基本概念和性质

3.1、红黑树的基本定义 

1. 每个结点不是红色就是黑色
2. 根节点是黑色的 
3. 如果一个节点是红色的，则它的两个孩子结点是黑色的 
4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点 
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

 3.2、红黑树性质的要点

• 根节点是黑色的
• 不能有两个相连的红色节点。这意味着从任意节点到其子节点的路径上不能出现连续的红色节点，以避免出现不平衡情况
• 从任意节点出发，到达其每个叶子节点的路径上的黑色节点数量必须相同。这确保了树的高度始终保持在一个合理的范围内，从而保证了高效的查找操作
• 空节点（NIL节点）被认为是黑色的。这样可以确保每个路径上的黑色节点数量相等，即使是经过了空节点的路径。
• 性质3和性质4我们可以推出一个红黑树中最长路径应该是最短路径的二倍，最短路径：全为黑，最长路径：一黑一红
   

我们需要注意的是空节点（NIL节点）被认为是黑色的，从任意节点出发，到达其每个叶子节点的路径上的黑色节点数量必须相同

 4、红黑树的效率

4.1 红黑树效率

红黑树的查找，插入和删除操作，时间复杂度都是O(logN)

4.2 红黑树和AVL树的比较

• AVL树的时间复杂度虽然优于红黑树，但是对于现在的计算机，cpu太快，可以忽略性能差异
• 红黑树的插入删除比AVL树更便于控制操作
• 红黑树整体性能略优于AVL树，红黑树旋转情况少于AVL树

5、对旋转的基本理解 

在数据结构中，旋转是一种常见的操作，用于调整树或其他数据结构的结构以保持平衡或满足某些性质。在红黑树、AVL树、二叉搜索树等数据结构中，旋转操作通常用于平衡树的结构，以确保高效的插入、删除和查找操作。旋转操作有两种基本类型：左旋和右旋

5.1、左旋

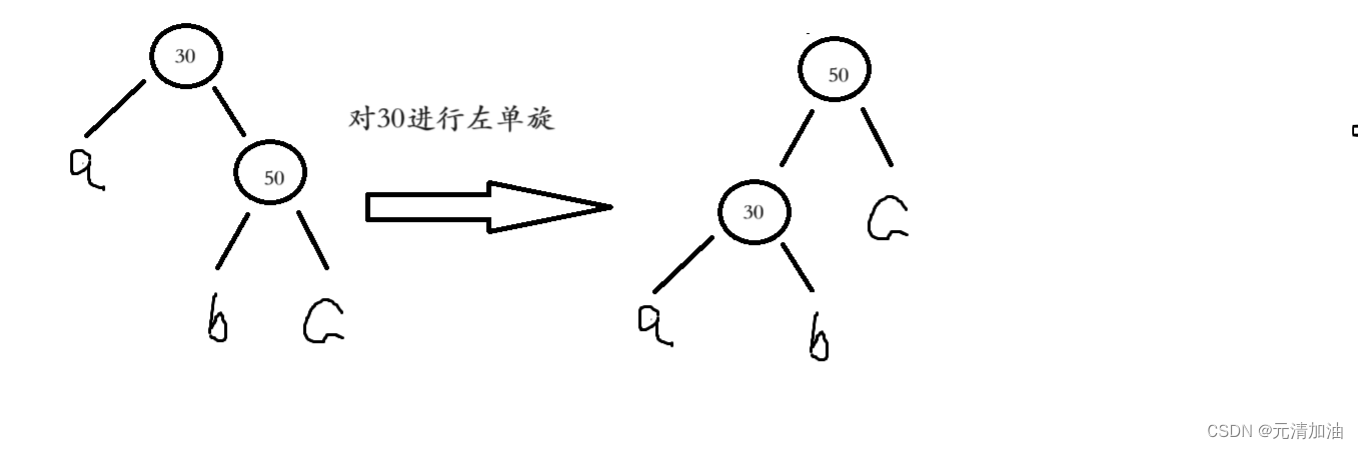
左旋是一种将某个节点的右子节点旋转上来的操作。它会将当前节点下移，并且将其右子节点提升为新的父节点。这可以用于解决树向右倾斜的情况，以保持树的平衡。左旋的基本步骤：

• parent:30
• subR:50
• subRL:b

1. subRL变成parent的右子树 
2. parent变成subR的左子树
3. subR变成新根

 5.2、右旋

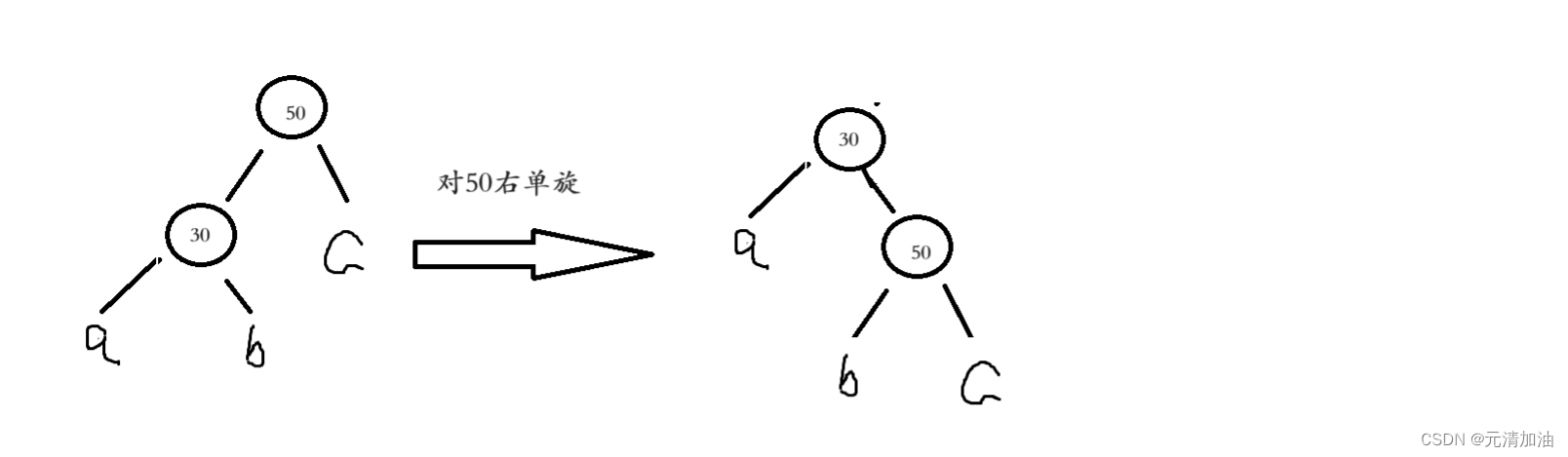
• 50为parent，30为subL，b为subLR 

1. subLR变成parent的左子树 
2. parent变成subL的右子树
3. subL变成新根

5.3、代码展示

template<class K, class V>
void AVLTree<K, V>::RotateL(Node* parent)  //左旋
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* parentParent = parent->_parent;parent->_parent = subR;if (subRL)subRL->_parent = parent;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}}template<class K, class V>
void AVLTree<K, V>::RotateR(Node* parent)  //右旋
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent)   //parent就是根，无需向上调整{_root = subL;subL->_parent = nullptr;}else                  //parent不是根，继续向上调整{if (parentParent->_left == parent){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}}

 6、红黑树的插入操作

1. 按照二叉搜索的树规则插入新节点
2. 检测新节点插入后，红黑树的性质是否造到破坏

因为新节点的默认颜色是红色，因此：如果其双亲节点的颜色是黑色，没有违反红黑树任何

性质，则不需要调整；但当新插入节点的双亲节点颜色为红色时，就违反了性质三不能有连

在一起的红色节点，此时需要对红黑树分情况来讨论：

约定 :cur 为当前节点， p 为父节点， g 为祖父节点， u 为叔叔节点

• 情况一: cur为红，p为红，g为黑，u存在且为红

• 情况二: cur为红，p为红，g为黑，u不存在/u存在且为黑

• 情况三: cur为红，p为红，g为黑，u不存在/u存在且为黑

6.1、情况一

情况一: cur为红，p为红，g为黑，u存在且为红

解决方式：将p,u改为黑，g改为红，然后把g当成cur，继续向上调整

1. 如果g是根节点，调整完后要将g变为黑色
2. 如果g不是根节点，继续向上调整

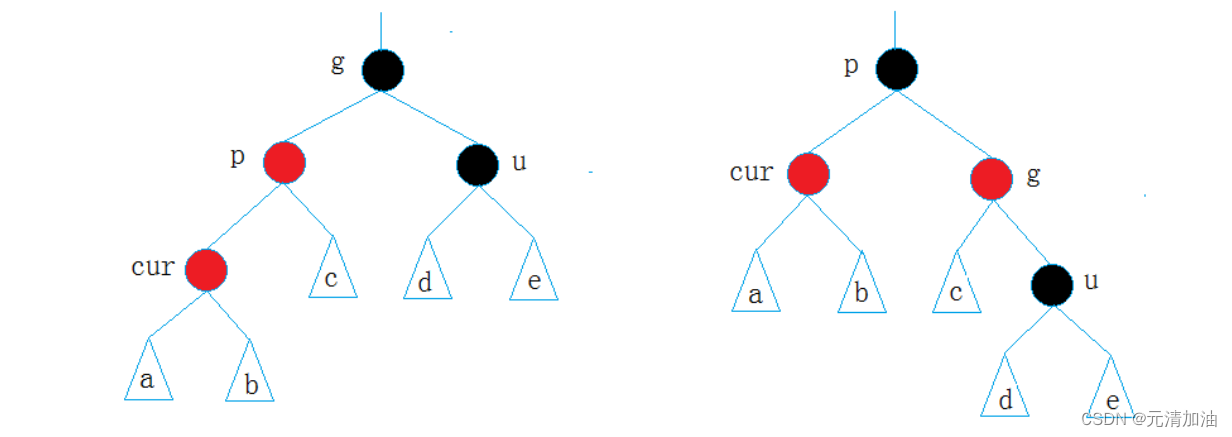
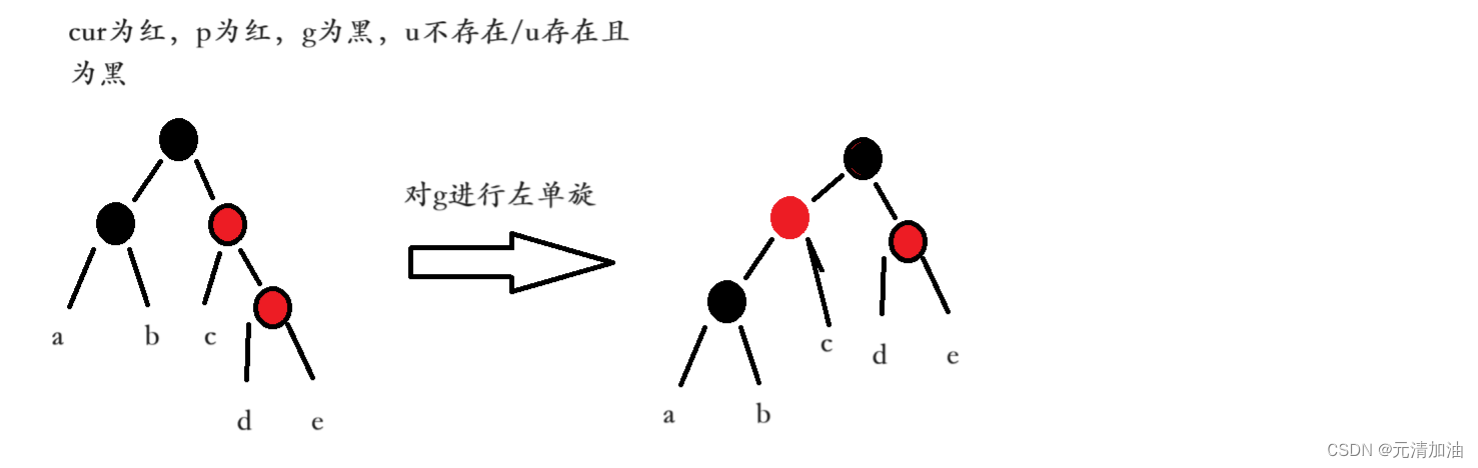
6.2、情况二

情况二: cur为红，p为红，g为黑，u不存在/u存在且为黑

解决方式：p为 g 的左孩子， cur 为 p 的左孩子，则对g进行右单旋转；相反，

                  p为g 的右孩子， cur 为 p的右孩子，则对g进行左单旋转

                  p、g 变色 --p 变黑， g 变红

6.3、情况三

情况三: cur为红，p为红，g为黑，u不存在/u存在且为黑

解决方式：p为 g 的左孩子， cur 为 p 的右孩子，则针对 p做左单旋转，再对g进行右单旋转；相反，

                  p为g 的右孩子， cur 为 p 的左孩子，则针对 p做右单旋转，再对g进行左单旋转

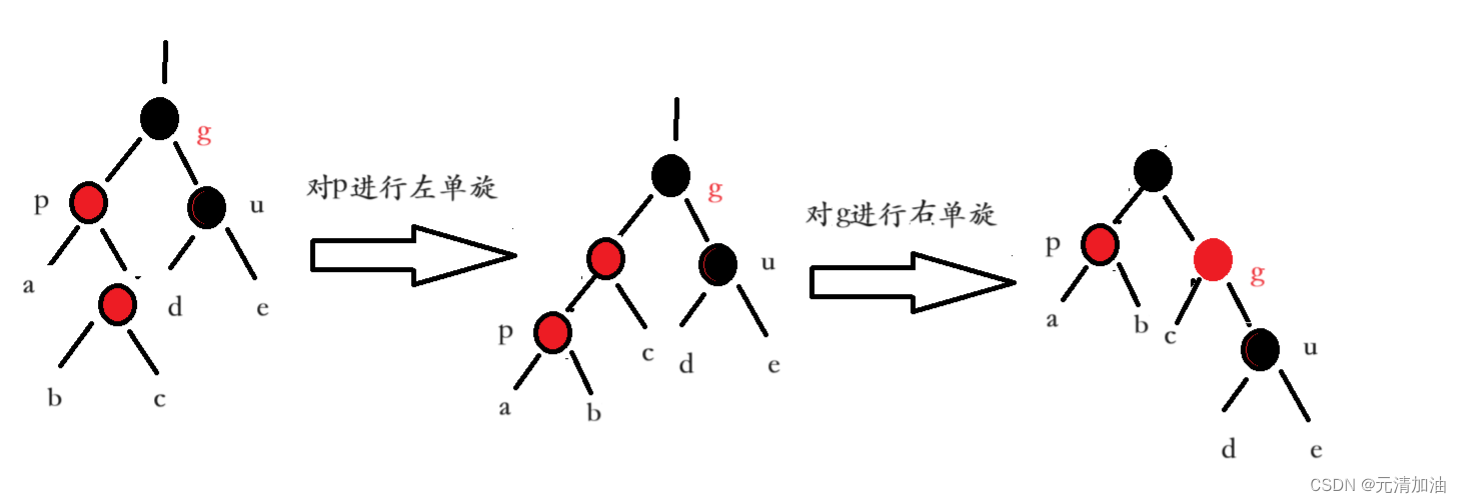
6.4、插入代码展示

template<class K, class V>
bool RBTree<K,V>::Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}// 新增节点给红色cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){//     g//   p   u// cNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上更新处理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){// 单旋//     g//   p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// 双旋//     g//   p//     cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else  // parent == grandfather->_right{//     g//   u   p //          c//Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//     g//   u   p //     c//RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;
}