图中任意两点之间的最短路径问题

Dijkstra和Bellman-Ford也可以以所有点为源点，求出任意两点之间的最短距离，但是Dijstra不能解决带负权的的边，Bellman-Ford 效率慢点

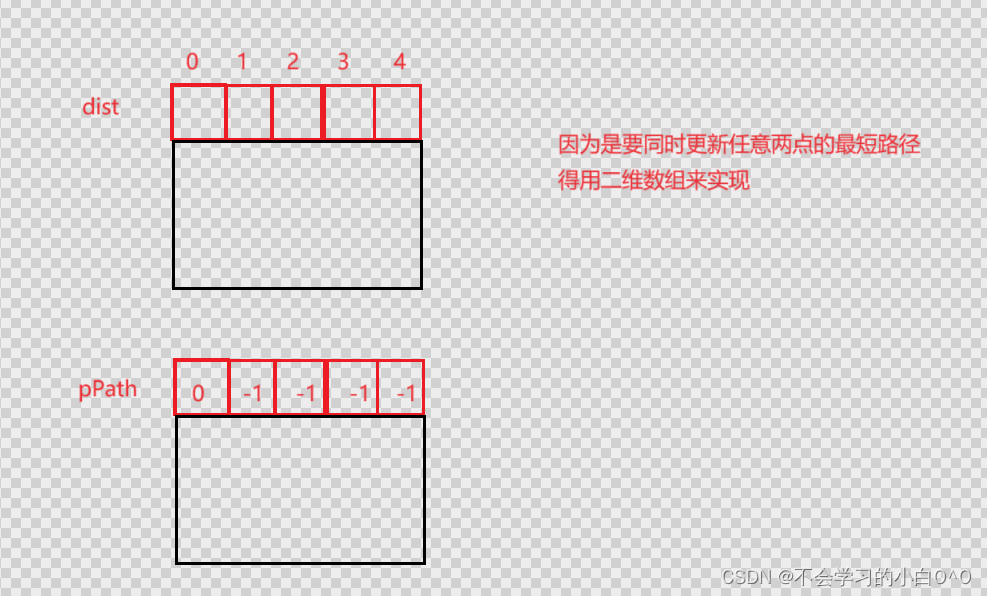
Floyd算法考虑的是一条最短路径的中间节点，即简单路径p={v1 ， v2,  ...  ,vn}上除v1和vn的任意节点

设K是p的一个中间节点，那么从i到 j 的最短路径就被分成 i到 k 和 k 到 j 的两段最短路径p1和p2，p1是从 i到 k且中间节点属于 {1  ，2  ，... , k-1}取得的一条最短路径，p2是从k到  j 且中间节点属于{1  ，  2 ， ...  ,k-1}取得的一条最短路径

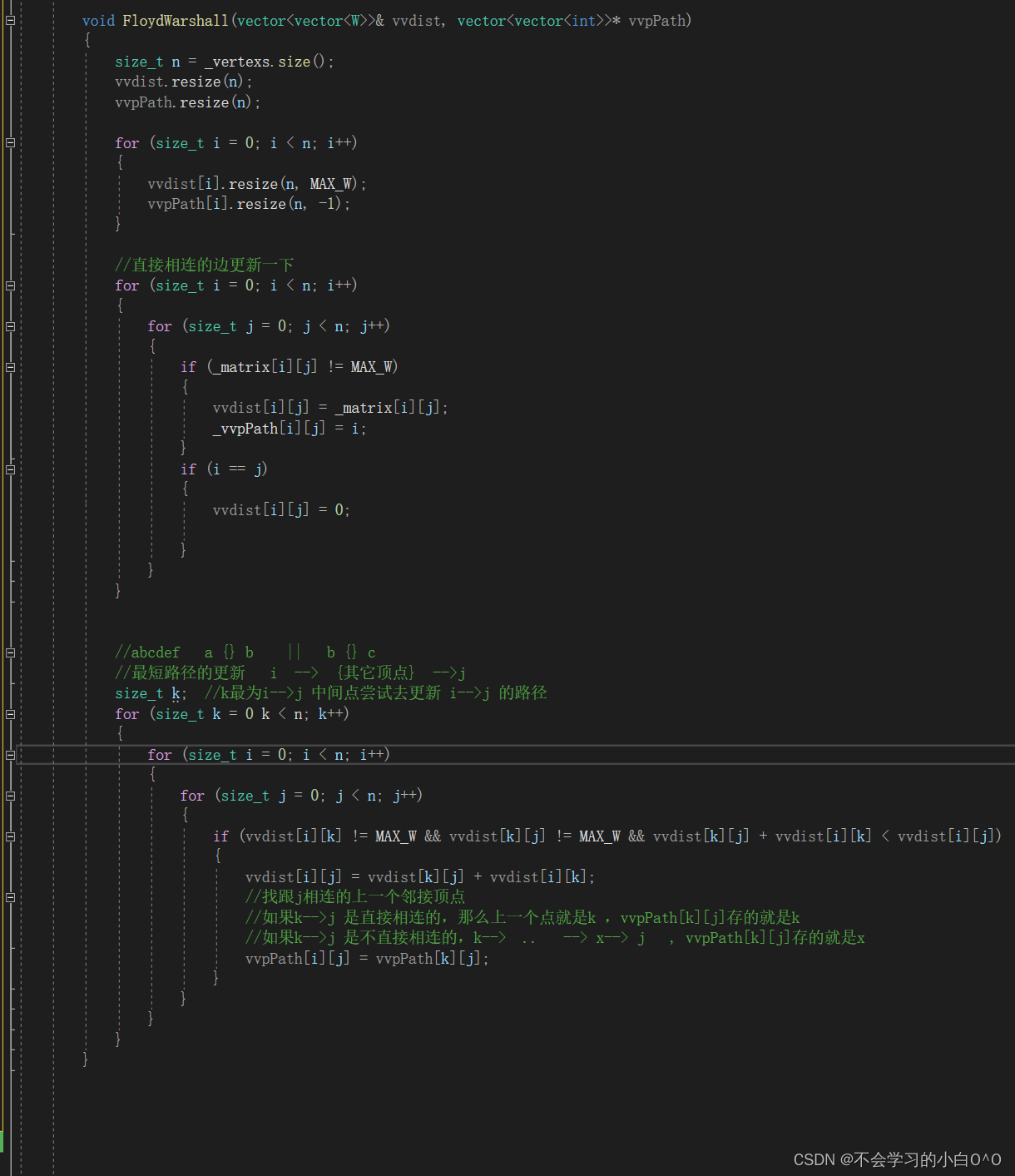
Floyd-Warshall算法的原理是动态规划

设Di，j ，k为从i到j的只以（1..k）集合中的节点为中间节点的最短路径长度

        1.若最短路径经过点k ，则Di，j，k = Di，k ，k-1  + Di，j ，k-1

        2.若最短路径不经过点k，则Di，j，k=Di，j，k-1

因此 ， Di，j，k = min（Di，k ，k-1  ，Di，j ，k-1  +  Di，j，k-1）