目录

前言

最短通路

迪杰斯特拉( Dijkstra )算法

1.算法步骤 

2.代码实现

3.算法分析

弗洛伊德( Floyd )算法

1.算法步骤

2.代码实现

3.算法分析

---

前言

        今天我们接着学习图的应用，最短通路问题，所谓的最短通路就是求从一个点到另一个点最短路径。那这里我们可以去通过Dijkstra算法去实现，这个算法思路比较绕，但是下面我会去详细讲解。

最短通路

典型用途:交通网络的问题一一从甲地到乙地之间是否有公路连通?

在有多条通路的情况下，哪一条路最短?

交通网络用有向网来表示:

顶点——表示地点；

弧——表示两个地点有路连通；

弧上的权值——表示两地点之间的距离、交通费或途中所花费的时间等。

如何能够使一个地点到另一个地点的运输时间最短或运费最省?这就是一个求两个地点间的最短路径问题。

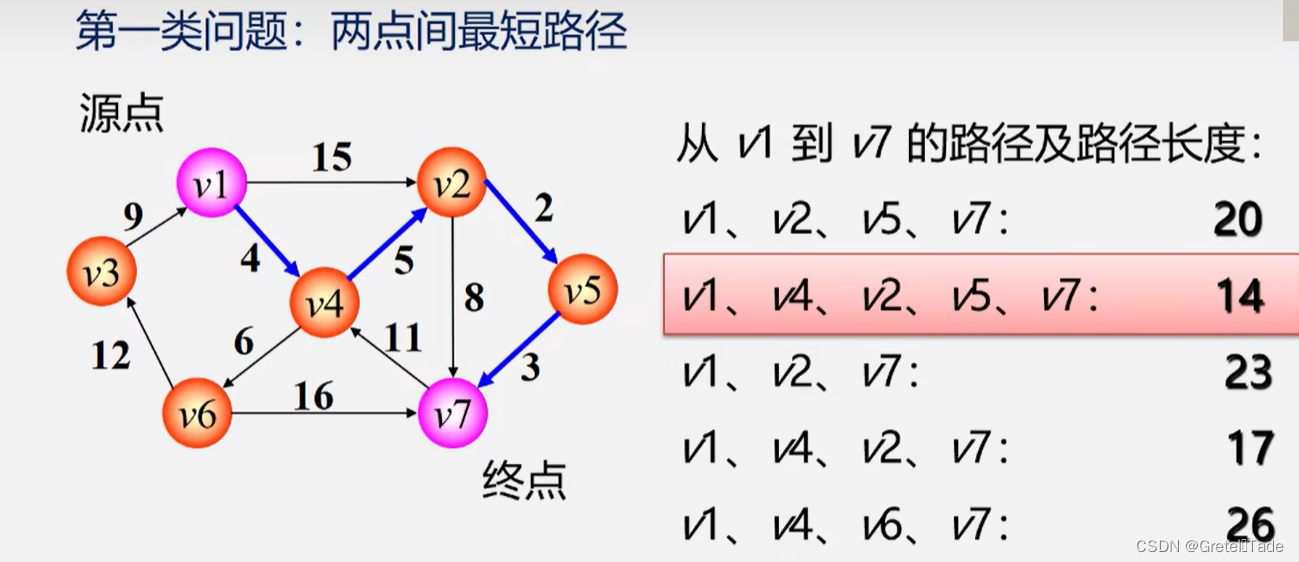
问题抽象：在有向网中A点（源点)到达B点（终点)的多条路径中，寻找一条各边权值之和最小的路径，即最短路径。

        最短路径与最小生成树不同，路径上不一定包含 n个顶点，也不定包含 n-1条边

（1）

 （2）

两种常见的最短路径问题:

• 单源最短路径一用Dijkstra（迪杰斯特拉）算法
• 所有顶点间的最短路径—用Floyd(弗洛伊德）算法

下面我就分别介绍这两种算法。 

迪杰斯特拉( Dijkstra )算法

Dijkstra 算法，是由荷兰计算机科学家 Edsger Wybe Dijkstra 在1956年发现的算法，戴克斯特拉算法使用类似广度优先搜索的方法解决赋权图的单源最短路径问题。Dijkstra 算法原始版本仅适用于找到两个顶点之间的最短路径，后来更常见的变体固定了一个顶点作为源结点然后找到该顶点到图中所有其它结点的最短路径，产生一个最短路径树。本算法每次取出未访问结点中距离最小的，用该结点更新其他结点的距离。需要注意的是绝大多数的Dijkstra 算法不能有效处理带有负权边的图。

1.算法步骤 

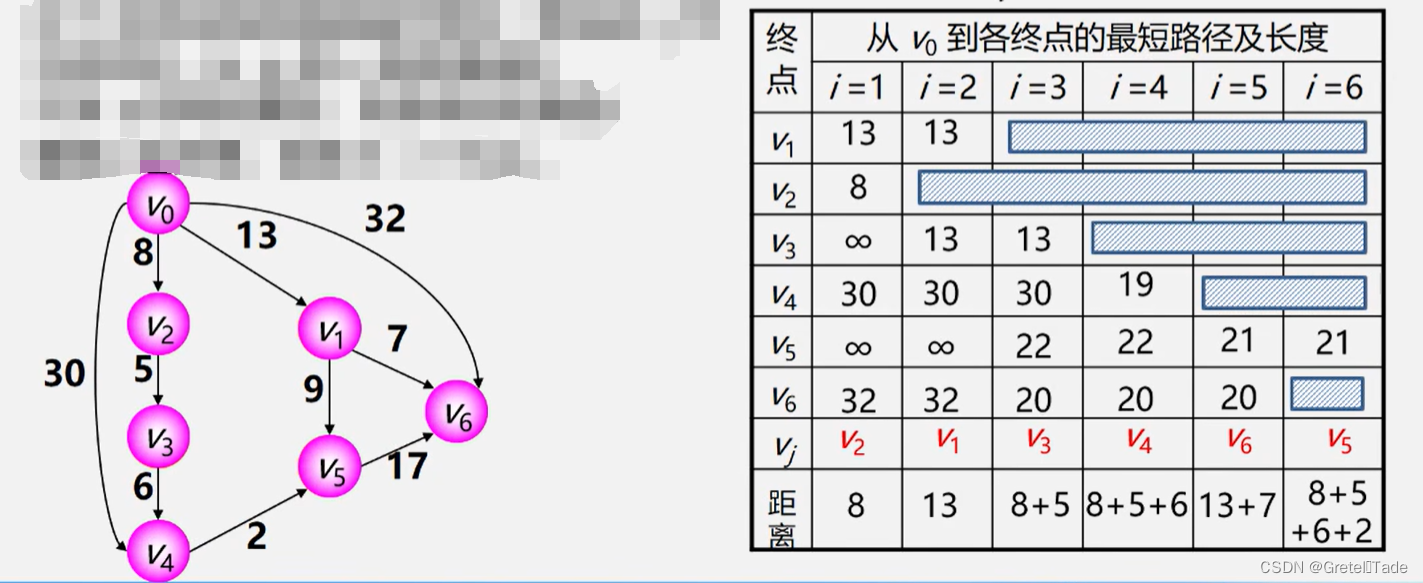
1. 初始化:先找出从源点vo到各终点v,的直达路径(vo,vk) ,即通过一条弧到达的路径。
2. 选择:从这些路径中找出一条长度最短的路径（vo,u)
3. 更新:然后对其余各条路径进行适当调整:
   • 若在图中存在弧(u,vk)，且(v0,u) + (u,vk)<(v0,vk),
   • 则以路径（v0,u;vk)代替(v0,vk)。

在调整后的各条路径中，再找长度最短的路径，依此类推。

图例： 

2.代码实现

代码思路：

对应这个算法，我们如何去写这个代码呢？

        首先需要三个数组，分别是path、dis_min、comp，这三个数组作用分别是记录起点遍历过的每一个位置、记录起点到其他顶点最近的距离，集合U中到其他顶点的距离（集合U初始化为起点，每次遍历一个点就把这个点加入到集合U）

        然后在集合U当中找到起点到其他顶点的最近距离，返回这个顶点的位置和路径长度，分别存入到path和dis_min当中，然后把这个新的顶点加入到集合U，更新comp数组即可。

邻接矩阵的相关结构：

#define Maxint 32767
#define Maxnum 100//最大顶点数//数据类型
typedef struct d {char id[10];//……
}
ElemType;
//图的邻接数组
typedef struct graph {ElemType vexs[Maxnum];//图数据int matrix[Maxnum][Maxnum];//二维数组int vexnum;//点数int arcnum;//边数
}Graph;

Dijkstra算法代码：

//距离最近顶点的结构体：
typedef struct node {int index;//下标int dis;//到这个顶点的距离
}Nearest;
//comp找到最近的顶点
Nearest find_min(int* comp,int n) {Nearest loca_min;//初始化,找到comp中第一个不为-1的数据for (int j = 0; j < n; j++) {if (comp[j] != -1) {loca_min.dis = comp[j];loca_min.index = j;break;}}//找到comp当前最小值的顶点for (int i = 0; i < n; i++) {if (comp[i]!=-1) {if (loca_min.dis > comp[i]) {loca_min.index = i;loca_min.dis = comp[i];}}}return loca_min;
}//Dijkstra算法
void Dijkstra(Graph G, char* start_id) {printf("(Dijkstra算法)起始点到其他顶点最短路径:\n");int* dis_min = (int*)malloc(sizeof(int) * G.vexnum);//起点到其他顶点记录最短路径int* path = (int*)malloc(sizeof(int) * G.vexnum);//记录遍历的顺序过程int* comp= (int*)malloc(sizeof(int) * G.vexnum);//当前集合U内，起点与其他顶点的距离//初始位置int start = Locate_vex(G, start_id);//初步处理for (int i = 0; i < G.vexnum; i++) {path[i] = -1;comp[i] = G.matrix[start][i];}int count = 0;path[count] = start;dis_min[count] = 0;comp[start] = -1;//标记为-1，表示这个点已经在集合U当中count++;//后继处理for (int i = 0; i < G.vexnum-1; i++) {Nearest loca_min= find_min(comp,G.vexnum);int k= loca_min.index;int new_mindis = loca_min.dis;//把找到最近新的点，相关数据放入到path和dis_min当中path[count] = loca_min.index;dis_min[count] = loca_min.dis;count++;comp[k] = -1;//标记这个顶点已经加入集合U//输出，起点到这个点最近距离结果printf("%s->%s %d\n", G.vexs[start].id,G.vexs[k].id,new_mindis);//comp数组更新比较for (int j = 0; j < G.vexnum; j++) {if (comp[j]!=-1) {if (comp[j] > G.matrix[k][j] + new_mindis) {comp[j] = G.matrix[k][j] + new_mindis;}}}}//输出path路径for (int i = 0; i < G.vexnum; i++) {printf("%s ", G.vexs[path[i]].id);}//释放空间free(dis_min);free(path);free(comp);dis_min = path = comp = NULL;
}

输入这个图相关边和点的数据：

测试结果：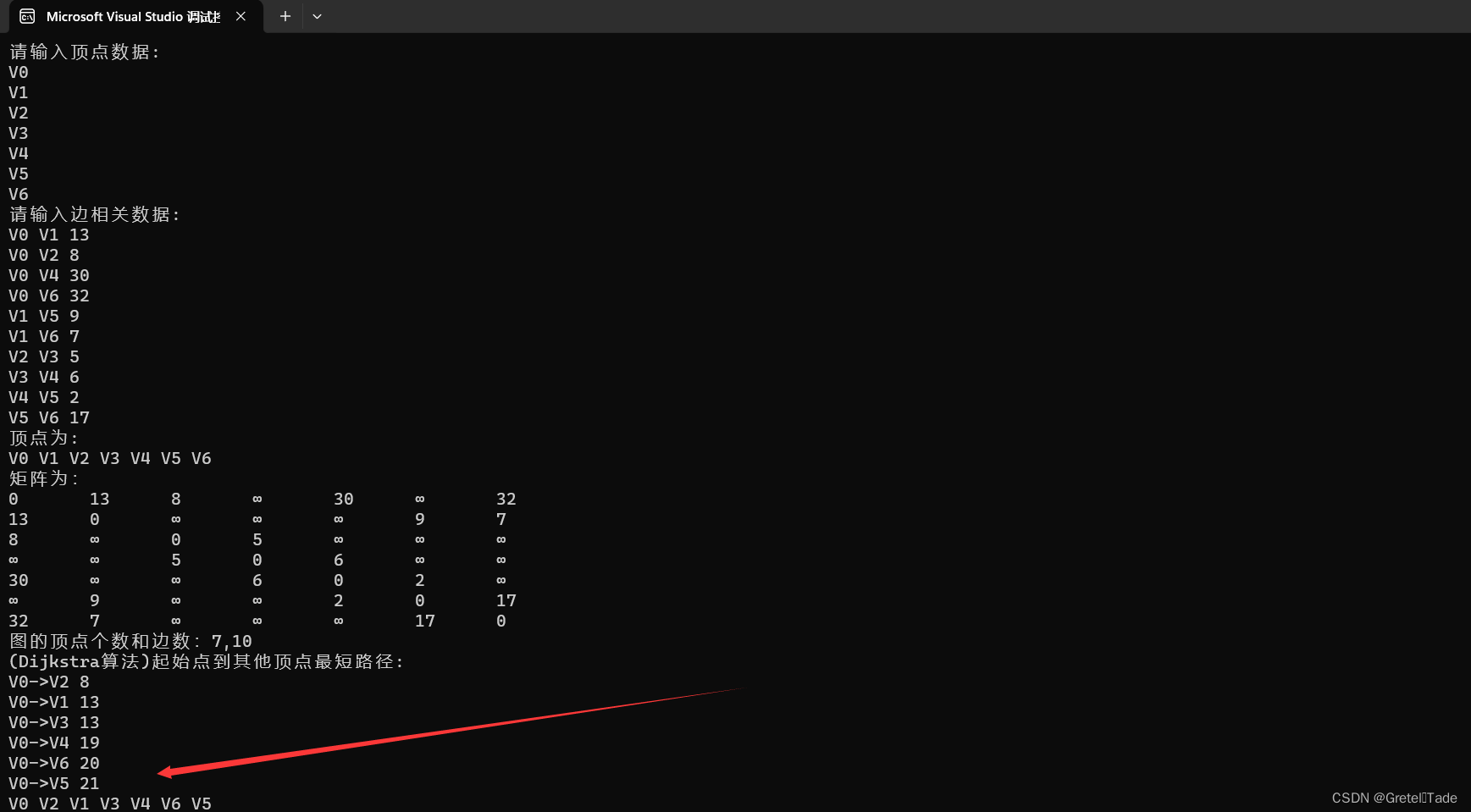

3.算法分析

设图有n个顶点，e条边

时间复杂度：O(n^2)

空间复杂度:O(n)

弗洛伊德( Floyd )算法

        Dijkstra适用于非负权图，并且一次只能从网络中找源点到任何一个节点的最短路径，而Floyd算法的应用更加广泛，可以求网络中任意两点之间的最短路径，而且弗洛伊德算法适用于负权图，这篇文章就用图和表的形式来介绍一下弗洛伊德算法！

1.算法步骤

算法思想

• 逐个顶点试探
• 从vi,到vj的所有可能存在的路径中
• 选出一条长度最短的路径

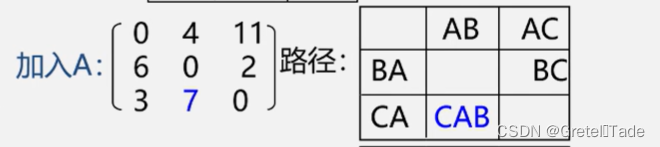
求最短路径步骤: 

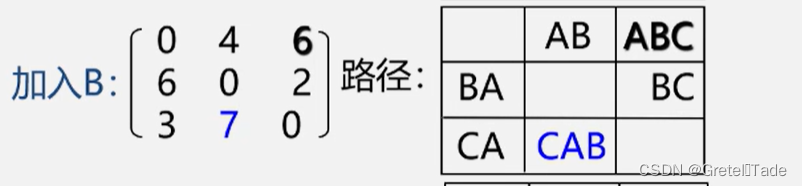
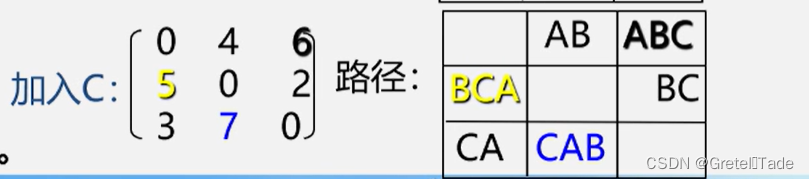
1.         初始时设置一个n阶方阵,令其对角线元素为0，若存在弧<Vi,Vj>，则对应元素为权值;否则为oo。
2.         逐步试着在原直接路径中增加中间顶点，若加入中间顶点后路径变短，则修改之;否则，维持原值。所有顶点试探完毕，算法结束

过程如下：

 

2.代码实现

//Floyd算法
void Floyd(Graph G) {Graph V = G;//图V作为修改图，存放每一个顶点找到其他顶点最近距离for (int i = 0; i < G.vexnum; i++) {int add = i;//向其中加入第add个顶点for (int j = 0; j < G.vexnum; j++) {//起始顶点for (int k = 0; k < G.vexnum; k++) {//目标顶点if (V.matrix[j][k] > V.matrix[j][add] + G.matrix[add][k])V.matrix[j][k] = V.matrix[j][add] + G.matrix[add][k];}}}//打印图V的矩阵print_matrix(V);printf("\nFloyd算法结果如下:\n");for (int i = 0; i < V.vexnum; i++) {for (int j = i; j < V.vexnum; j++) {printf("%s->%s min_distance:%d\n", V.vexs[i].id, V.vexs[j].id,V.matrix[i][j]);}}
}

3.算法分析

设当前图有n个顶点，你条边

时间复杂度：O(n^3)

 

以上就是本期的全部内容了，喜欢的话给个赞吧！

分享一张壁纸：