1、题目

问题描述

小蓝和小桥上完课后，小桥回顾了课上教的树形数据结构，他在地上画了一棵根节点为 1 的树，并且对每个节点都赋上了一个权值 $w_i$。

小蓝对小桥多次询问，每次询问包含两个整数 $x,k$，表示询问节点为 $x$ 的所有 $k$ 层子节点中，最大值是多少。

我们称节点 $v$ 为 $x$ 的 $k$ 层子节点满足：

1. $v$ 是 $x$ 为根的子树中的节点。
2. $de{p}_v-de{p}_x=k$，$de{p}_v$ 为 $v$ 在树中的深度。

例如：

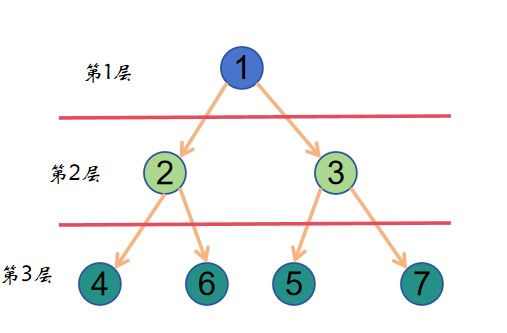
{2, 3} 为 1 号点的 1 层子节点，{4, 5, 6, 7} 为 1 号点的 2 层子节点，{4, 6} 为 2 号点的 1 层子节点。

输入格式

第一行输入两个正整数 $n,q$，表示树的节点数量和询问数量。

第二行输入 $n$ 个正整数 $w_1,w_2,...,w_n$，表示每个点的权值。

接下来 $n-1$ 行，每行输入两个整数 $v_i,u_i$，表示存在一条由 $v_i$ 指向 $u_i$ 的边。

接下来 $q$ 行，每行输入两个整数 $x,k$，表示询问 $x$ 的 $k$ 层子节点中，最大值是多少。

输出格式

输出 $q$ 行，每行输出一个整数，表示每个询问的最大值。

样例输入

7 4
2 9 8 7 8 6 4
1 2
1 3
2 4
2 6
3 5
3 7
1 2
1 1
3 1
2 1

样例输出

8
9
8
7

说明

样例如下图：

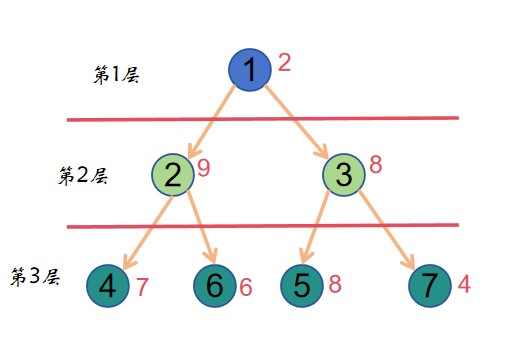
数据范围

• $1\le v_i,u_i,k,x\le n\le 10^5$
• $1\le w_i\le 10^9$
• $1\le q\le 10^5$
• 数据保证是一棵以 1 为根的有向树，并且每次询问的 $k$ 一定合法。

原题链接

小蓝的疑问

2、思路

考察数据结构（堆，线段树），图（DFS序），二分查找

1. 离线做法：启发式合并 + 优先队列，同时对于每层的节点都维护一个大根堆，每次询问，查询堆中最大值。时间复杂度：$O(nlo{g}^{2}n)$。
2. 在线做法：DFS序 + 线段树（ST表）+ 二分查找，对每层按照 DFS 序相对顺序建立线段树（或者 ST 表），当查询到 $u$ 时，通过二分找到 $k$ 层的左右端点，查询最大值。时间复杂度：$O(nlogn)$。

3、代码

• 强制合并

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <assert.h>
using namespace std;typedef long long ll;
const int N = 1e5 + 100;
const int MOD = 998244353;vector<int> G[N];
int n, q;
int w[N];
int Siv[N], Son[N], ans[N];typedef pair<int, int> Pair;vector<Pair> query[N];priority_queue<Pair> Dep[N];int DFN = 0, rdn[N], dfn[N], dep[N];
int vis[N];int ddep[N];void dfs(int u, int fa = 0, int dpt = 1) {ddep[u] = dpt;Siv[u] = 1;for (int v : G[u]) {if (v == fa) continue;dfs(v, u, dpt + 1);ddep[u] = max(ddep[u], ddep[v]);Siv[u] += Siv[v];if (Siv[v] > Siv[Son[u]]) Son[u] = v;}
}void to_get_ans(int u, int fa = 0, int dpt = 1, bool clr = false) {dfn[u] = ++DFN;rdn[dfn[u]] = u;dep[u] = dpt;for (int v : G[u]) {if (v == fa || v == Son[u]) continue;to_get_ans(v, u, dpt + 1, false);}if (Son[u]) {to_get_ans(Son[u], u, dpt + 1, true);}int ed = dfn[u];if (Son[u]) ed = dfn[Son[u]] - 1;for (int i = dfn[u]; i <= ed; ++i) {int vv = rdn[i];Dep[dep[vv]].push({w[vv], vv});vis[vv] = true;}// cout << endl;for (Pair q : query[u]) {int k = q.first;assert(k + dpt <= ddep[u]);int id = q.second;while (Dep[k + dpt].size() && vis[Dep[k + dpt].top().second] == 0) {Dep[k + dpt].pop();}ans[id] = Dep[k + dpt].top().first;}if (!clr) {int ed = dfn[u] + Siv[u];for (int i = dfn[u]; i < ed; ++i) {vis[rdn[i]] = false;}}}void sol() {cin >> n >> q;for (int i = 1; i <= n; ++i) {cin >> w[i];}   int u, v; for (int i = 1; i < n; ++i) {cin >> u >> v;G[u].push_back(v);G[v].push_back(u);}dfs(1);int x, k;for (int i = 1; i <= q; ++i) {cin >> x >> k;query[x].push_back({k, i});}to_get_ans(1);for (int i = 1; i <= q; ++i) {cout << ans[i] << '\n';}
}int main() {int T = 1;while (T--) {sol();}exit(0);
}

• 面向对象

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <assert.h>
#include <cmath>using namespace std;typedef long long ll;
const int N = 1e5 + 100;vector<int> G[N], val[N], dfsQ[N];
int w[N], n, q;
int DFN = 0, dfn[N], dep[N], Siv[N], MaxDpt = 0;class RMQ_t {
public:RMQ_t(const vector<int>& init);~RMQ_t();int query(int l, int r) const {int k = log2(r - l);return max(f[k][l], f[k][r - (1 << k)]);}
private:int **f;const int N, LOGN;
};RMQ_t *res[N];void dfs(int u, int fa = 0, int dpt = 1) {MaxDpt = max(MaxDpt, dpt);dfn[u] = ++DFN; dep[u] = dpt;Siv[u] = 1;val[dpt].push_back(w[u]);dfsQ[dpt].push_back(dfn[u]);for (int v : G[u]) {if (v == fa) continue;dfs(v, u, dpt + 1);Siv[u] += Siv[v];}
}void sol() {cin >> n >> q;for (int i = 1; i <= n; ++i) {cin >> w[i];}   int u, v, x, k; for (int i = 1; i < n; ++i) {cin >> u >> v;G[u].push_back(v);G[v].push_back(u);}dfs(1);for (int i = 1; i <= MaxDpt; ++i) {res[i] = new RMQ_t(val[i]);}while (q--) {cin >> x >> k;int l = lower_bound(dfsQ[k + dep[x]].begin(),dfsQ[k + dep[x]].end(),dfn[x]) - dfsQ[k + dep[x]].begin();int r = lower_bound(dfsQ[k + dep[x]].begin(),dfsQ[k + dep[x]].end(),dfn[x] + Siv[x]) - dfsQ[k + dep[x]].begin();cout << res[k + dep[x]]->query(l,r) << endl;}
}int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int T = 1;while (T--) {sol();}exit(0);
}RMQ_t::RMQ_t(const vector<int>& init) : N(init.size()), LOGN(log2(init.size()) + 1) {f = new int*[LOGN];for (int i = 0; i < LOGN; ++i) {f[i] = new int[N];}for (int i = 0; i < N; ++i) {f[0][i] = init[i];}for (int i = 1; i < LOGN; ++i) {for (int j = 0; j + (1 << i) - 1 < N; ++j) {f[i][j] = max(f[i - 1][j], f[i - 1][j + (1 << (i - 1))]);}}
}RMQ_t::~RMQ_t() {for (int i = 0; i < LOGN; ++i) {delete[] f[i];}delete[] f;
}