本人是一个web前端开发工程师，主要是vue框架，整理了一些面试题，今后也会一直更新，有好题目的同学欢迎评论区分享 ;-）

web面试题专栏：点击此处

---

背景

WEB前端面试官：0.2+0.3是否等于0.5？
：）

好家伙，不按套路出牌，之前也没深究，但是既然重新学习一下，就记录一下，免得又忘记了。

分析问题

面试官是问你0.1+0.2，或者0.2+0.3的问题吗？
不是的，要是下次有个作妖的问你，0.x+0.y呢？
显然不是，他要问你的是原理~

0.1+0.2
// 0.30000000000000004
0.2+0.3
// 0.5

控制台运行如下：

---

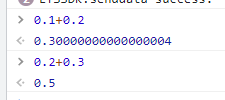
原理

死记硬背~~~。

1. 在浏览器的JavaScript环境中，遵循IEEE 754标准，就算记不全，也要记得IEEE（理科生搞得跟文科生一样，真蛋疼。。。）
2. 这个标准规定了浮点数的二进制表示以及浮点数的运算规则。
3. JavaScript中的Number类型就是基于这个标准实现的。因此，JavaScript中的浮点数遵循IEEE 754标准的规定，也会出现浮点数精度问题。

总的来说：IEEE754标准下，浮点数是用二进制进行存储运算的，部分十进制小数转成二进制是一个无限循环的数值，运算的时候会造成精度丢失。

---

复现

在浏览器环境中以IEEE754存储的0.1、0.2、0.3 咱们可以直接在控制台打印出来。

0.1.toString(2);
0.2.toString(2);
0.3.toString(2);

控制台运行如下：

---

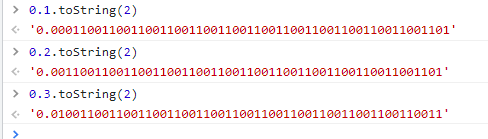
十进制小数转二进制

方法：小数乘2取整，直到没有小数为空，最后取整的数值进行正向排列就得到了。
以0.1 为例：

数值取整0.1 * 2 = 0.200.2 * 2 = 0.400.4 * 2 = 0.800.8 * 2 = 1.610.6 * 2 = 1.210.2 * 2 = 0.400.4 * 2 = 0.800.8 * 2 = 1.610.6 * 2 = 1.210.2 * 2 = 0.400.4 * 2 = 0.800.8 * 2 = 1.610.6 * 2 = 1.21（无限循环）……

正向排列整理后： 0001100110011…

十进制证书转二进制

方法：整数除2取余，直到整数为0，最后取余的数值进行倒叙排列就得到了。
以6为例：

数值余数6 / 2= 3 % 003 / 2 = 1 % 111 / 2 = 0 % 11

倒叙排列整理后： 110