1. 题目解析

LeetCode链接

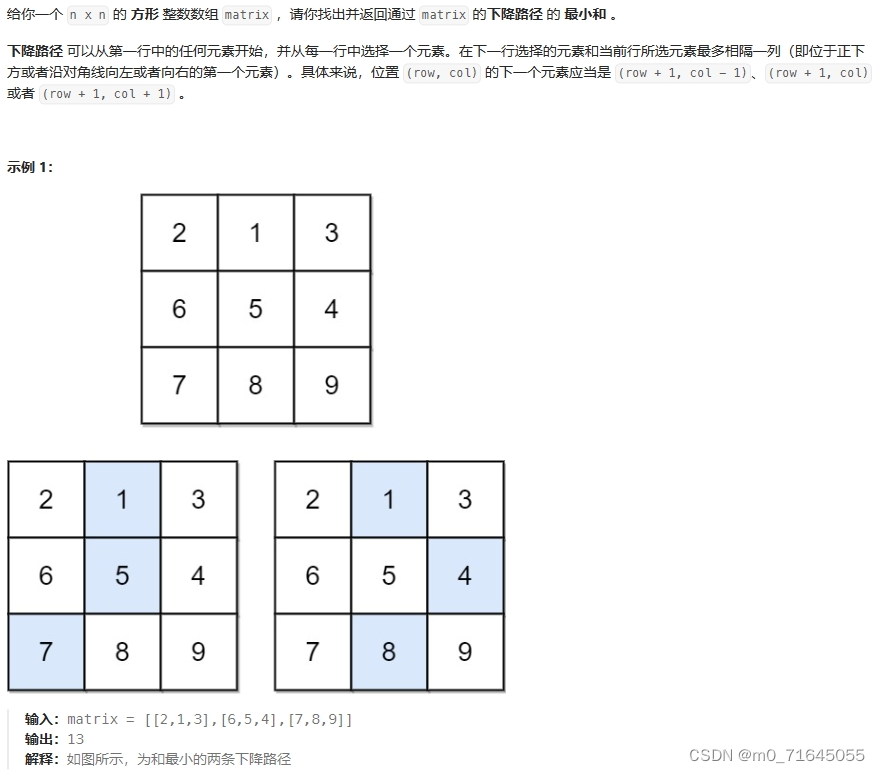
根据题目可以得出，当处于 [i][j] 位置时只能从 [i - 1][j - 1]，[i - 1][j]，[i - 1][j + 1] 这三个位置到达， 所以我们想要得到当前最小的路径和只需要得到上述三个位置的最小值加上该位置的值即可。

2. 解题思路

通过分析题目我们可以使用动态规划来解决这道题
首先我们要确定一下状态表示：
由于题目要求的是到达该位置的最小路径和， 所以我们可以用 dp[i][j] 来表示到达 [i, j] 位置时的最小路径和
然后就是确定状态转移方程：
状态转移方程一般都是从到达该点的最近一步得到

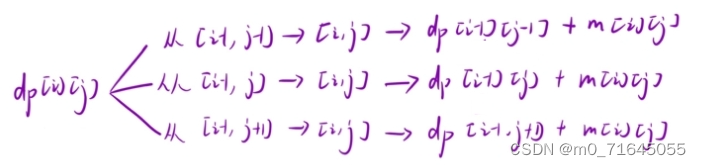
根据上述分析可以得出：
dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i - 1][j + 1])) + matrix[i - 1][j - 1]

最后是对 dp 数组进行初始化：
当我们在处理一些边界条件时可能会造成数组越界，所以我们可以创建一些虚拟节点来防止数组越界。
在创建虚拟节点时我们需要注意两个问题：

1. 填入的值要保证不影响结果的准确性
2. 要处理好下标的映射关系
   
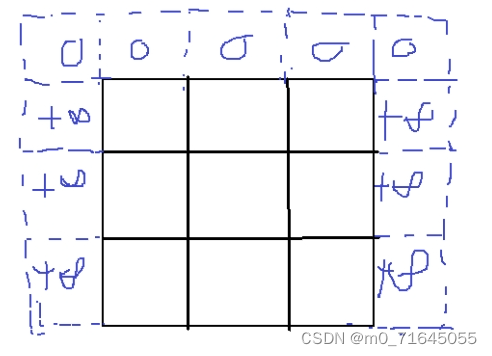
   为了保证第一行的准确性所以我们需要将最上边初始化为 0
   因为我们取的是上一行三个数的最小值所以在初始化在第一列和最后一列时不能设置为 0 而是要初始化为一个较大的数，这样才能保证不影响结果的准确性。

3. 代码实现

class Solution {public int minFallingPathSum(int[][] matrix) {int n = matrix.length;int[][] dp = new int[n + 1][n + 2];for (int i = 1; i <= n; i++) {dp[i][0] = dp[i][n + 1] = Integer.MAX_VALUE;}for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i - 1][j + 1])) + matrix[i - 1][j - 1];}}int min = Integer.MAX_VALUE;for (int i = 1; i <= n; i++) {if (dp[n][i] < min) {min = dp[n][i];}}return min;}
}