题目：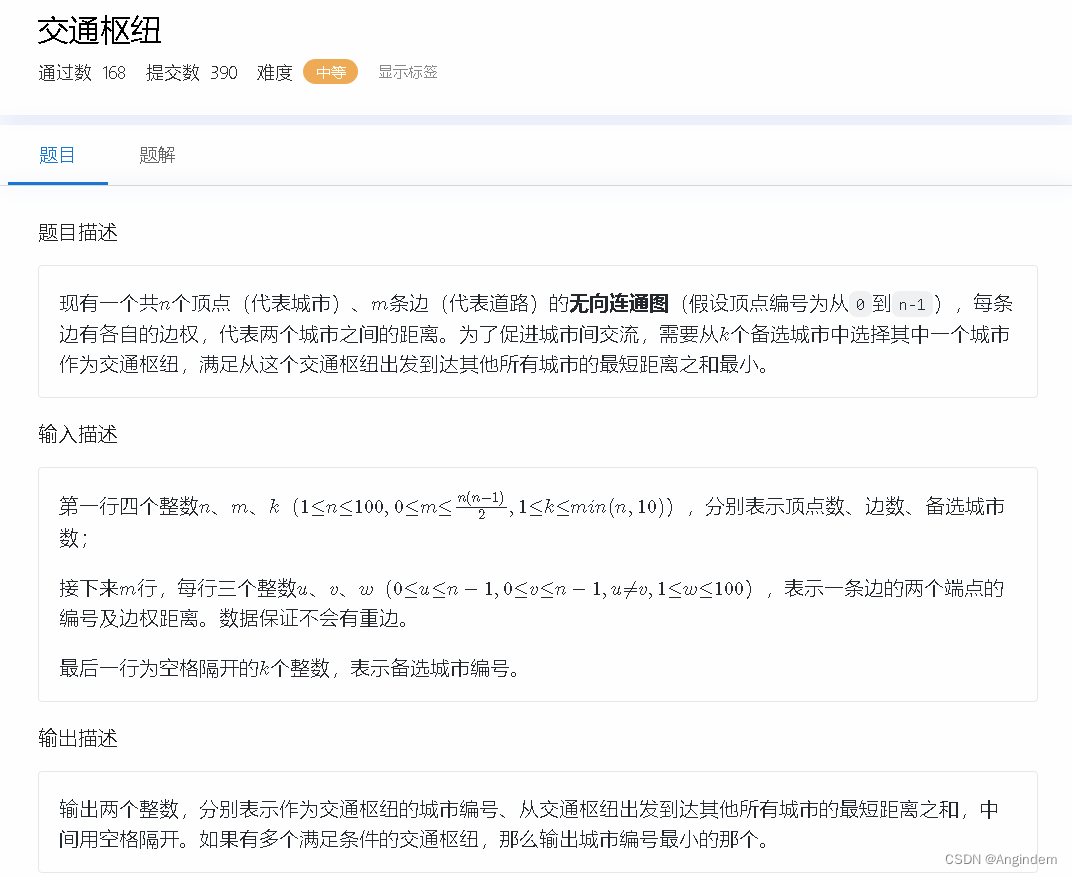

样例：

4 5 2
0 1 1
0 2 5
0 3 3
1 2 2
2 3 4
0 2

思路：

        由题意，绘制了该城市的地图之后，由给出的 k 个编号作为起点，求该点到各个点之间的最短距离之和最小的点是哪个，并输出该点，和该点到各个点之间的最短距离之和。

        这又是一个多起点多终点的题型，所以用 Floyd 算法非常的有效率。

代码详解如下：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <unordered_map>
#define endl '\n'
#define x first
#define y second
#define mk make_pair
#define int long long
#define NO puts("NO")
#define YES puts("YES")
#define umap unordered_map
#define INF 0x3f3f3f3f
#define All(x) (x).begin(),(x).end()
#pragma GCC optimize(3,"Ofast","inline")
#define ___G std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10,M = 500;
using PII = pair<int,int>;int n,m,k;int dist[M][M];	// 定义各个点之间的最短距离数组// 初始化各个点之间的最短距离
inline void Init()
{memset(dist,INF,sizeof dist);// 自身点之间的距离是 0for(int i = 0;i <= n;++i){dist[i][i] = 0;}
}inline void Floyd()
{// 这一层是中间点for(int k = 0;k < n;++k){// 这一层是 i 点for(int i = 0;i < n;++i){// 这一层是 j 点for(int j = 0;j < n;++j){// 更新选取最短的 i 到 j 的最短距离方案 ，即 i 到 k  ，k 再到 jdist[i][j] = min(dist[i][j],dist[i][k] + dist[k][j]);}}}
}// 由 x 点到各个点之间的最短距离之和
inline int DistSum(int x)
{int sum = 0;for(int i = 0;i < n;++i){sum += dist[x][i];}return sum;
}inline void solve()
{	cin >> n >> m >> k;Init();	// 初始化最短路距离数组while(m--){int a,b,c;cin >> a >> b >> c;// 记录两个点之间的最短距离，min 防止自环dist[a][b] = dist[b][a] = min(dist[a][b],c);}// 开始求各个点之间的最短距离Floyd();PII ans = {-1,-1};	// 答案城市编号，已经答案城市到各个点之间的最短距离之和while(k--){int a;cin >> a;	// 获取城市编号点int distSum = DistSum(a);	// 求最短距离之和if(ans.x == -1) ans = {a,distSum};	// 记录第一个点else if(ans.y > distSum) ans = {a,distSum};	// 更新更短的最短距离之和的点做 交通枢纽}// 输出答案cout << ans.x << ' ' << ans.y << endl;
}
signed main()
{
//	freopen("a.txt", "r", stdin);
//	___G;int _t = 1;
//	cin >> _t;while (_t--){solve();}return 0;
}

最后提交：