740. 删除并获得点数 - 力扣（LeetCode）

简单分析一下:

每一个数字其实只有2个状态选 or 不

可得预处理每一个数初始状态(不选为0,选为所有x的个数 * x)累加即可

for(auto &x : nums)dp[x][1] += x;

每选一个树 i 删去 i + 1 和 i - 1

故我们可以将 i - 1视为 i 的父节点, i + 1视为 i 的子节点(此时思路就向树形dp经典题"参加舞会"一样如果i节点参与,其子节点和父节点不参与)

可得

 for(int i = 2; i <= n;i++){dp[i][1] += dp[i - 1][0];dp[i][0] += dp[i - 1][1];}

再考虑特殊情况:中间断层 1 5 or 任意不连续数字串 

此时对与5 显然 其没有父节点 和 子节点(无法正常转移)

那么倒退4,我们构建4节点,因为其本身不存在选和不选都不影响最终结果

可得

            if(!dp[i][1]){dp[i][1] = dp[i][0] = mx;continue;}

由于每一个节点的权值大小不同,对于第i个节点为true的时候有特殊情况(即选的权值不如不选的情况)

可得

                dp[i][1] = max(dp[i][1] + dp[i - 1][0], dp[i - 1][1]);dp[i][0] += dp[i - 1][1];

由于题目数据范围为

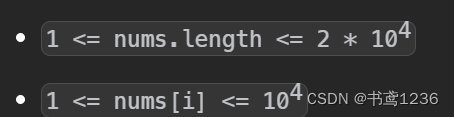
故进行转移时只用转移1e4次即可 

//using i64 = int64_t;
class Solution {
public:const int maxn = 1e4 + 10;int dp[10010][2];int deleteAndEarn(vector<int>& nums) {//视为树形dp(easy版)//例如:样例一 == >> 2 3 4//样例二 == >> 4 9 4    memset(dp, 0, sizeof dp);for(auto &x : nums)dp[x][1] += x;int mx = 0;for(int i = 1; i <= 10000; i++){if(!dp[i][1]){dp[i][1] = dp[i][0] = mx;continue;}else{dp[i][1] = max(dp[i][1] + dp[i - 1][0], dp[i - 1][1]);dp[i][0] += dp[i - 1][1];}mx = max({mx,dp[i][1],dp[i][0]});}return max(dp[10000][1], dp[10000][0]);}
};

 时间复杂度:常数级

2251. 花期内花的数目 - 力扣（LeetCode）