朴素NeRF中直接采用频率变换来做位置编码，为的是避免空间相邻采样点在MLP表示中的过平滑问题。比如位置(237, 332, 198)和位置(237,332,199)这两个点作为MLP的输入，MLP可能对个位不够敏感，导致输出过平滑的问题。例如：

由于缺乏位置编码，导致纹理相近区域的细节会丢失。
我们来看一下原文中关于Position Encoding的公式：
$$\gamma (p)=\left(\sin \left(2^0\pi p\right),\cos \left(2^0\pi p\right),\cdots ,\sin \left(2^{L-1}\pi p\right),\cos \left(2^{L-1}\pi p\right)\right)\text{\hspace{1em}(1)}$$
频率编码，很像傅里叶变换，代码如下：

import torchclass FreqEmbedder:def __init__(self, multires, include_input=True, input_dims=3, log_sampling=True):self.multires = multiresself.input_dims = input_dimsself.include_input = include_inputself.log_sampling = log_samplingself.periodic_fns = [torch.sin, torch.cos]self.embed_fns = Noneself.out_dim = Noneself.create_embedding_fn()def create_embedding_fn(self):embed_fns = []d = self.input_dimsout_dim = 0if self.include_input:embed_fns.append(lambda x: x)out_dim += dmax_freq = self.multires - 1N_freqs = self.multiresif self.log_sampling:freq_bands = 2. ** torch.linspace(0., max_freq, steps=N_freqs)else:freq_bands = torch.linspace(2. ** 0., 2. ** max_freq, steps=N_freqs)for freq in freq_bands:for p_fn in self.periodic_fns:embed_fns.append(lambda x, p_fn=p_fn, freq=freq: p_fn(x * freq))out_dim += dself.embed_fns = embed_fnsself.out_dim = out_dimdef embed(self, inputs):return torch.cat([fn(inputs) for fn in self.embed_fns], -1)

其中torch.sin和torch.cos实现的就是数学意义的功能，举个例子：

import torch
pi = 3.1415926
degree_30 = pi / 6 # 30 degreea = torch.Tensor([degree_30])
r = torch.sin(a)
print(r) # tensor([0.5000])

上面实验表明了$sin(30°)=\frac{1}{2}$；

对于频率位置编码：假设一个位置的$x_0=30$，它相邻的位置是$x_1=31$，经过$r=sin(x\ast 512)$编码以后，$x_0$编码后的位置为$-0.6842$，而$x_1$编码后的位置为$0.6240$。差距一目了然。
这里的512则表示频率，如公式（1）所示的$2^{L-1}\pi$。

当然，也如公式（1）所示，我们并不以单一的频率来表示位置编码，比如我们挨个用$[1,2,4,8,16,32,64,128,256,512]$这10种频率来表示编码位置（只需用公式$r=sin(p\ast x)$，然后简单concat到一起）。这就完成了基本的位置编码。当然，我们还可以加入相位平移，把$cos(p\ast x)$的结果也concat到一起。

所以，对于一个位置$p(x,y,z)$，我们用10种频率（如$[1,2,4,8,16,32,64,128,256,512]$）来编码，每种频率采用两种相位（sin和cos），那编码后的位置应该有$3\times 10\times 2=60$维来表示原始的三维坐标向量。通常，我们会把原始的三维坐标向量也concat到一起，那么就输出$60+3=63$维，直接喂到MLP里去。

众所周知，NeRF除了位置$(x,y,z)$输入外，还需要输入观测角度$(\theta ,\varphi )$。观测角度可以用ray direction来表示，通常采用三维向量。也需要进行编码，也可以统称为位置编码。我们用同样的方法，但可以少用一些频率，比如我们用$[1,2,4,8]$这四种频率来编码观测角度。编码后的维度也可计算出来：$3\times 4\times 2+3=27$。

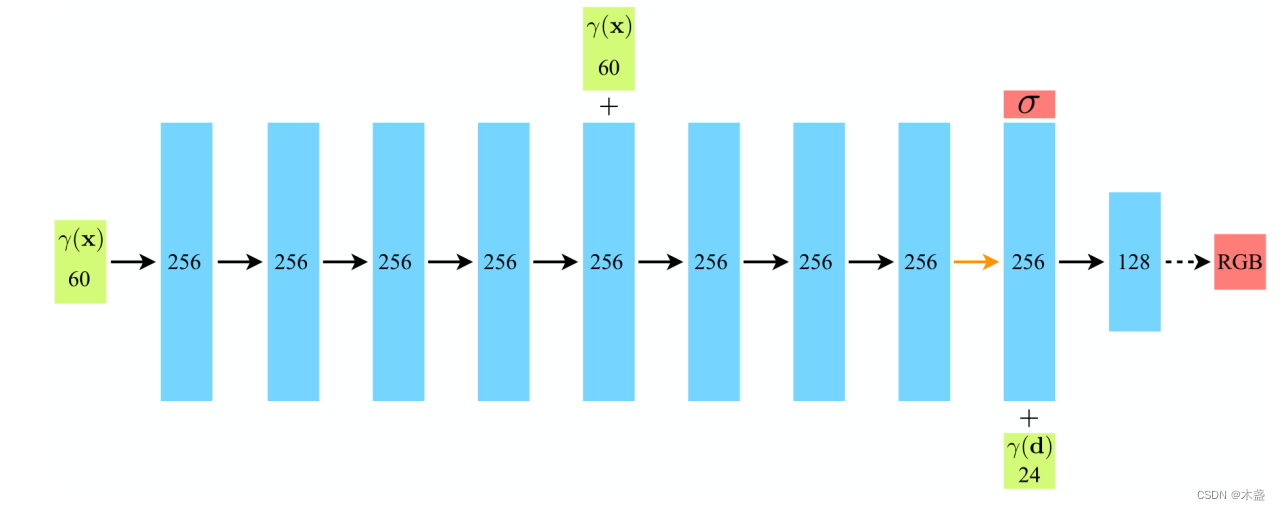
上图就是NeRF中MLP的输入顺序，图中并没有加原始位置，所以位置编码的维度为60，而方向编码的维度为24。输入阶段一目了然～

本文内容由本人亲自整理，如有疑问请留言交流～