最长上升子序列

dp解法：

f[i]表示以i结尾的最长上升子序列的长度

按照倒数第二个选谁分类：

我们先扫描i号元素前的每个元素（正向），找出第一个比i号元素小的元素k号。①仍然选i号元素，f[i]。②选k号，f[k]+1

但是，这种解法时间复杂度为O(N^2)，一但长度到200，就会扣分，我们这次就讨论O(nlog n)的算法。

不升子序列最小划分数

我们用贪心解决这个问题。定义d[i]为第i条不升子序列的最后一个数，cnt代表有几个子序列

我们先扫描每个数字x[i]，再枚举每一个子序列，判断是否能接在某个子序列后，如果不行，则新增一个序列即可。

#include <bits/stdc++.h>
#define N 1005
using namespace std;
int n,i,j,d[N],x[N];
int main(){cin>>n;for(int i=0;i<n;i++) cin>>x[i];int cnt=0;for(i=0;i<n;i++){for(j=0;j<cnt;j++)if(d[j]>=x[i]) break;d[j]=x[i];if(j==cnt) cnt++;}cout<<cnt<<endl;return 0;
}

但是这个算法时间复杂度也是O(N^2)，我们要进行优化

我相信，聪明的你们一定能想到二分查找

#include <bits/stdc++.h>
#define N 1005
#define INF 2e9
using namespace std;
int n,d[N],x[N];
int main(){cin>>n;for(int i=0;i<n;i++) cin>>x[i];fill(d,d+n,INF);for(i=0;i<n;i++)*lower_bound(d,d+n,x[i])=x[i];int cnt=lower_bound(d,d+n,INF)-d;cout<<cnt<<endl;return 0;
}

Dilworth反链

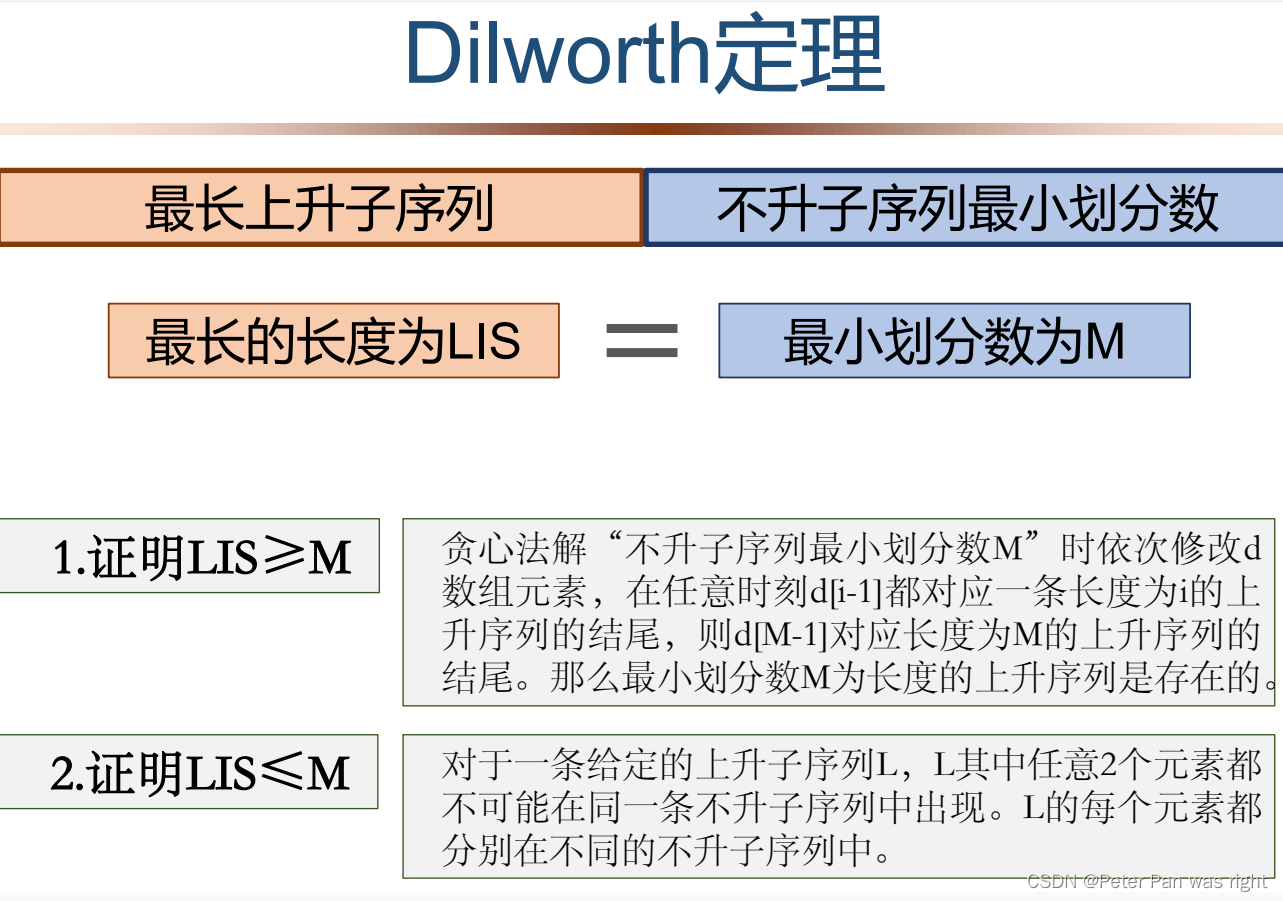
LIS为最长子序列， 那么说明一定能找到LIS个数，从左往右是递增的。那么这些树一定不能放在同一组内，不然与不升矛盾。到目前为止，每个数单独为一组，已经开了LIS组了。说明任何一种满足要求的分组，组数都>=LIS。

所以，回到LIS，代码如下👇

#include <bits/stdc++.h>
#define N 1005
#define INF 2e9
using namespace std;
int n,d[N],x[N];
int main(){cin>>n;for(int i=0;i<n;i++) cin>>x[i];fill(d,d+n,INF);for(i=0;i<n;i++)*lower_bound(d,d+n,x[i])=x[i];int cnt=lower_bound(d,d+n,INF)-d;cout<<cnt<<endl;return 0;
}

*若为严格下降子序列最小划分，则把lower_bound变为upper_bound 

综合运用

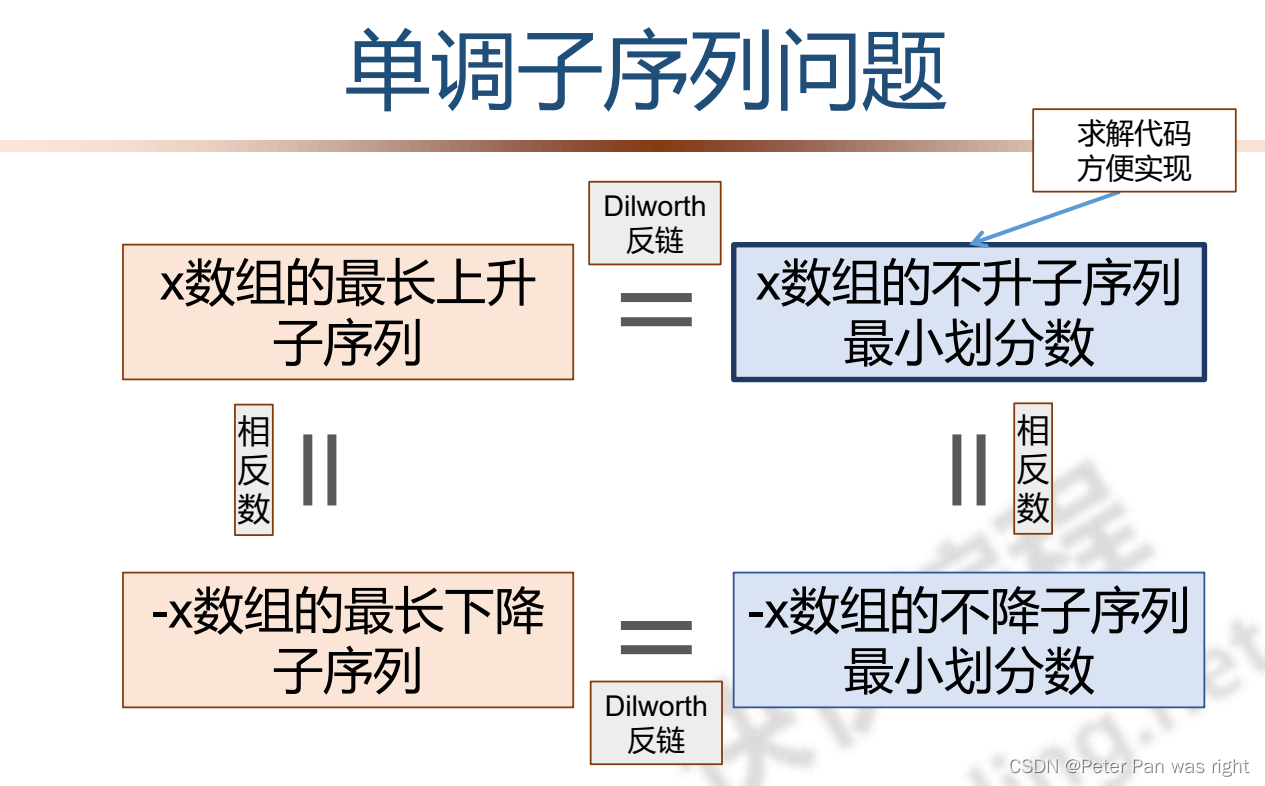
 希望这些对大家有用，三联必回