🕺作者： 主页

我的专栏C语言从0到1探秘C++数据结构从0到1探秘Linux菜鸟刷题集

😘欢迎关注：👍点赞🙌收藏✍️留言

🏇码字不易，你的👍点赞🙌收藏❤️关注对我真的很重要，有问题可在评论区提出，感谢阅读！！！

前言

本篇共4题，附有解题思路和AC代码。

边听歌边刷起来吧~

🎸Exhale

47. 全排列 II

链接：47. 全排列 II

解题思路

1. 在 travalBack 函数中，首先判断当前排列的长度是否等于原始数组的长度，如果是，则将该排列加入到结果集中，并返回。

2. 如果当前排列长度不满足条件，就遍历原始数组 nums 中的元素，并进行处理。

3. 在遍历过程中，如果当前元素与前一个元素相等，并且前一个元素没有被使用过，则跳过该元素，以避免产生重复的排列。

4. 如果当前元素没有被使用过，则将其加入到当前排列 path 中，并将该元素标记为已使用。

5. 然后递归调用 travalBack 函数，继续生成下一个位置上的元素。

6. 在递归调用返回后，需要将当前元素标记为未使用，并将其从当前排列中移除，以便生成其他可能的排列。

7. 在 permuteUnique 函数中，首先对原始数组进行排序，以确保重复元素紧邻。

8. 然后创建一个布尔型数组 used，并将其传递给 travalBack 函数进行全排列的生成。

9. 最后返回结果集 res。

AC代码

class Solution {
public:vector<vector<int>> res;vector<int> path; void travalBack(vector<int>& nums ,vector<bool>& used){if(path.size()==nums.size()){res.push_back(path);return;}for(int i=0;i<nums.size();++i){if(i>0&&nums[i-1]==nums[i]&&used[i-1]==false)continue;else if(used[i]==false){path.push_back(nums[i]);used[i]=true;travalBack(nums,used);used[i]=false;path.pop_back();}}}vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(),nums.end());vector<bool> used(nums.size());travalBack(nums,used);return res;}
};

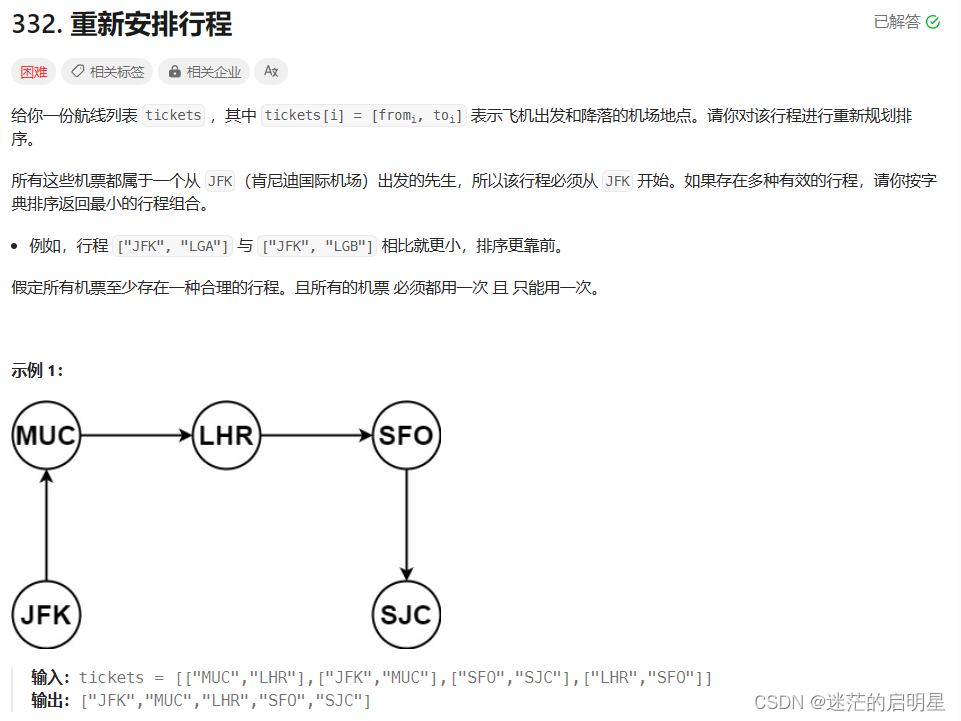
332. 重新安排行程

链接：332. 重新安排行程

解题思路

@代码随想录

这一题和之前的回溯一样的模板，它的关键点在于要看到怎么处理航班之间的关系，但是其实来说就是要判断行程是否合理，如果之前已经飞过，就不能再飞，还有就是整躺下来如果不能用到所有的机票也是不对的路径，还要注意的是要求字典序最小的路径

所以可以得出：

• 终止条件：result的大小需要等于机票的数量加1

• for循环内：需要判断是否有当前的机票，有则进入”可回溯“的区域

• ”可回溯“区域：注意票数的更新，如果满足条件就可以返回true，已经找到

• 在一开始的时候就要建立机场之间的映射关系

AC代码

class Solution {
public://unordered_map<出发机场, map<到达机场, 航班班次>> targets;unordered_map<string, map<string,int>> targets;bool backtraval(int ticketNum,vector<string>&result){if(result.size() == ticketNum + 1){return true;}for(pair<const string,int>&target : targets[result[result.size()-1]]){if(target.second > 0){result.push_back(target.first);target.second--;if(backtraval(ticketNum,result))return true;result.pop_back();target.second++;}}return false;}vector<string> findItinerary(vector<vector<string>>& tickets) {targets.clear();vector<string> result;for(const vector<string>&vec : tickets){targets[vec[0]][vec[1]]++;}result.push_back("JFK");backtraval(tickets.size(),result);return result;}
};

51. N 皇后

链接：51. N 皇后

解题思路

@代码随想录

AC代码

class Solution {
public:vector<vector<string>> res;void travalBack(int row,int n,vector<string>& board){if(row == n){res.push_back(board);return;}for(int col=0;col<n;++col){if(isvalid(row,col,n,board)){board[row][col]='Q';travalBack(row+1,n,board);board[row][col]='.';}}}bool isvalid(int row,int col,int n,vector<string>& board){for(int i=0;i<row;++i){if(board[i][col]=='Q')return false;}for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--){if(board[i][j]=='Q')return false;}for(int i=row-1,j=col+1;i>=0&&j<n;i--,j++){if(board[i][j]=='Q')return false;}return true;}vector<vector<string>> solveNQueens(int n) {std::vector<std::string> board(n, std::string(n, '.'));travalBack(0,n,board);return res;}
};

37. 解数独

链接：37. 解数独

解题思路

@代码随想录

AC代码

class Solution {
private:
bool backtracking(vector<vector<char>>& board) {for (int i = 0; i < board.size(); i++) {        // 遍历行for (int j = 0; j < board[0].size(); j++) { // 遍历列if (board[i][j] == '.') {for (char k = '1'; k <= '9'; k++) {     // (i, j) 这个位置放k是否合适if (isValid(i, j, k, board)) {board[i][j] = k;                // 放置kif (backtracking(board)) return true; // 如果找到合适一组立刻返回board[i][j] = '.';              // 回溯，撤销k}}return false;  // 9个数都试完了，都不行，那么就返回false }                }}return true; // 遍历完没有返回false，说明找到了合适棋盘位置了
}
bool isValid(int row, int col, char val, vector<vector<char>>& board) {for (int i = 0; i < 9; i++) { // 判断行里是否重复if (board[row][i] == val) {return false;}}for (int j = 0; j < 9; j++) { // 判断列里是否重复if (board[j][col] == val) {return false;}}int startRow = (row / 3) * 3;int startCol = (col / 3) * 3;for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复for (int j = startCol; j < startCol + 3; j++) {if (board[i][j] == val ) {return false;}}}return true;
}
public:void solveSudoku(vector<vector<char>>& board) {backtracking(board);}
};