[动态规划] (五) 路径问题: LeetCode 62.不同路径

62. 不同路径

题目解析

(1) 机器人从左上角到右下角有多少方法

(2) 机器人只能向左或者向右移动

(3) 求总共有多少种走路的方法

解题思路

状态表示

从题目+经验

我们暂时设dp[i] [j]：以(i, j)为终点，所到达i使用的方法的数量

状态转移方程

从题目解析中可以看出，dp(i, j)的值取决于dp(i-1, j)和dp(i, j-1)的值，因为机器人只能向右或者向下走。

且我们猜测的状态表达式正好是到达以(i, j)为终点的方法。

dp[i][j] = dp[i-1][j] + dp[i][j-1]

初始化和填表

• 初始化

我们在初始化时，发现第一排和第一列都是相同的特殊情况，需要处理。

这很麻烦，所以我们多开辟一列和一排。

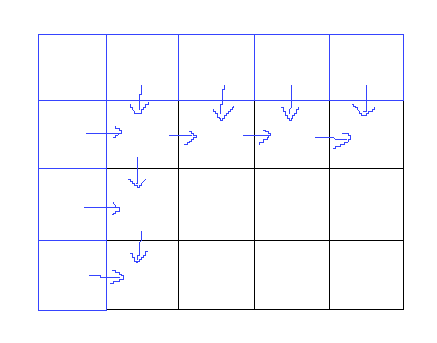
每一个格子都取决于前一个与上一个相加。

所以我们只需要初始化dp[0] [1] 或者 dp[1] [0] 为1即可。

• 填表

先填第一列，然后第二列，然后…

返回值

我们扩大了一列和一排，所以返回dp[m] [n]

看到这里，大家可以先去尝试实现代码，再来看下面的内容

代码实现

class Solution {
public:int uniquePaths(int m, int n) {//创建dp数组vector<vector<int>> dp(m+1, vector<int>(n+1));//初始化dp[1][0] = 1;//填表for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){dp[i][j] = dp[i-1][j] + dp[i][j-1];}}//返回值return dp[m][n];}
};

总结

细节1：初始化，只需要扩大一列和一排就可以初始化的很方便

细节2：下标需要移位。(i-1 , j-1) => (i , j)