crypto

week1 立正

逆序得到
:V Qook at you~ this is flag: EmxhE8tERKAfYAZ6S636dIWuEK46ZK4yRBdNdK4uRKd4 decode it
中间那串像b64
解码解不出什么 猜测还要rotate
Emxh 和 flag编码后的前几位比较接近
考虑大写字母需要继续偏移

对大写字母处理完后得到
:Q Look at you~ this is flag: ZmxhZ8tZMFVfTVU6N636dDRuZF46UF4yMWdIdF4uMFd4 decode it
解码得 flag�Y0U_MU:7��t4nd^:P^21gHt^.0Wx
对比flag{Y0U_base64编码ZmxhZ3tZMFVf和解出的前12位ZmxhZ8tZMFVf
数字也得继续偏移

a = ':V Qook at you~  this is flag: EmxhE8tERKAfYAZ6S636dIWuEK46ZK4yRBdNdK4uRKd4 decode it'
a = list(a)for i in range(len(a)):if a[i].isupper():a[i] = chr((ord(a[i]) - 65 - 5) % 26+65)if a[i].isdigit():a[i] = chr((ord(a[i]) - 48 + 5) % 10+48)print("".join(a))

解b64得到flag
flag{Y0U_MU57_5t4nd_uP_r1gHt_n0W}

[WEEK1]电信诈骗

真想不到
异或50后rot47

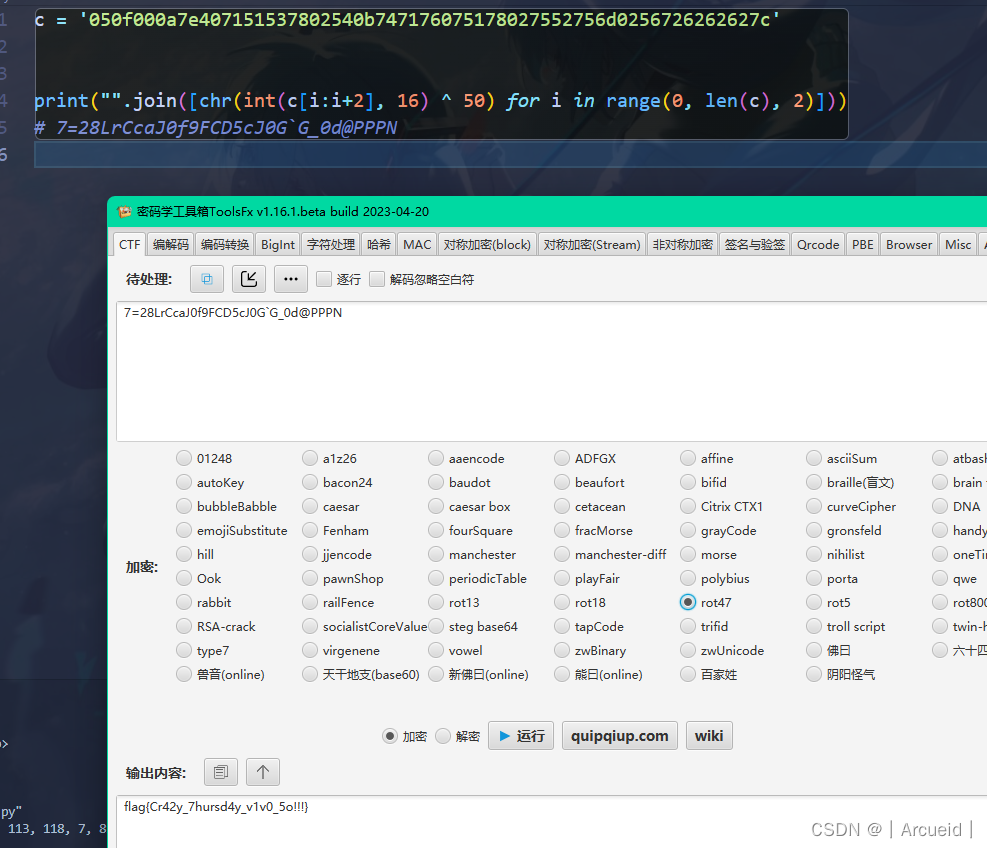
c = '050f000a7e407151537802540b747176075178027552756d0256726262627c'print("".join([chr(int(c[i:i+2], 16) ^ 50) for i in range(0, len(c), 2)]))
# 7=28LrCcaJ0f9FCD5cJ0G`G_0d@PPPN

马后炮来说的话 第四行第七列 卷土重来 还是可以联想到rot47的

[WEEK3]ECC

哎 当初导sympy包
里面有个对象叫EllipticCurve
完了老和我说构造函数有问题

from Crypto.Util.number import *
import gmpy2def crack_unknown_increment(states, modulus, multiplier):increment = (states[1] - states[0]*multiplier) % modulusreturn modulus, multiplier, incrementdef crack_unknown_multiplier(states, modulus):multiplier = (states[2] - states[1]) * \inverse(states[1] - states[0], modulus) % modulusreturn crack_unknown_increment(states, modulus, multiplier)hint = [1570694739893062645954897001702004554030820147773705206144961894236480600502144377530243430,1115071559941911318308753566664426840423418447339890011281946738239984044436490114276986358, 1724417937645231946682439402005218433918418922370889412352845326882349141006072218192190414]
N = 1756436166407836493798726314365345209041467063368466691280475314657490639743277323145836159N, A, B = (crack_unknown_multiplier(hint, N))rounds = 201
inv_a = gmpy2.invert(A, N)
seed = hint[0]
for i in range(rounds-2):seed = (inv_a*(seed - B)) % NE = EllipticCurve(GF(int(seed)), [A, B])
P=E(37977159917993725569055235995991171988930922261017470137494292644600863220268 , 18702328678557323528043531437349309255558505679181203523362701784535278781654 )
Q=E(50869218310545924409688834318827602878615827095578074934136681999097237356553 , 56112306156084592253561365078969255013878959268941761289693638560533128799289 )print(E.order())def SmartAttack(P, Q, p):E = P.curve()Eqp = EllipticCurve(Qp(p, 2), [ZZ(t) + randint(0, p)*p for t in E.a_invariants()])P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)for P_Qp in P_Qps:if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:breakQ_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)for Q_Qp in Q_Qps:if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:breakp_times_P = p*P_Qpp_times_Q = p*Q_Qpx_P, y_P = p_times_P.xy()x_Q, y_Q = p_times_Q.xy()phi_P = -(x_P/y_P)phi_Q = -(x_Q/y_Q)k = phi_Q/phi_Preturn ZZ(k)print(long_to_bytes(int(SmartAttack(P, Q, seed))))

[WEEK3]e=3

一开始以为p存在线性关系
像天山固网那道题样的
然后试了一下没出来就摆烂了

观察到N在M进制下易分解
我们用sage看看

from Crypto.Util.number import *N = 3298593732762513945346583663585189774036688951059270517149719979434109398447628726951796006700754759352430339647168415338320547665794785951232342902233013221132246450312038122695046634624323814318286314664160113738299465643128504110932989263063331290006313
c = 869489491924953293290699796392271834401780578884556874640489836779925847562085802848542382525324081900560761299059365684697233025590164192409062717942292142906458498707677300694595072310705415037345581289469698221468377159605973403471463296806900975548438
M = 2**54
k = 6
digit = M
digits = N.digits(digit)
f = 0
for i, each in enumerate(digits):f += each * x ^ iprint(f)

分解得到pqr
后面就是有限域开方

from Crypto.Util.number import *N = 3298593732762513945346583663585189774036688951059270517149719979434109398447628726951796006700754759352430339647168415338320547665794785951232342902233013221132246450312038122695046634624323814318286314664160113738299465643128504110932989263063331290006313
c = 869489491924953293290699796392271834401780578884556874640489836779925847562085802848542382525324081900560761299059365684697233025590164192409062717942292142906458498707677300694595072310705415037345581289469698221468377159605973403471463296806900975548438
M = 2**54
k = 6
e = 3
digit = M
digits = N.digits(digit)
f = 0
for i, each in enumerate(digits):f += each * x ^ i# print(f.factor)
p = (54595*x ^ 5 + 17296*x ^ 4 + 5814*x ^ 3 + 36787*x ^ 2 + 58035*x + 45247)
q = (25282*x ^ 5 + 31957*x ^ 4 + 31998 *x ^ 3 + 6834*x ^ 2 + 31014*x + 33821)
r = (350*x ^ 5 + 48522*x ^ 4 + 12574*x ^ 3 + 35367*x ^ 2 + 47153*x + 11459)p = int(p(M))
q = int(q(M))
r = int(r(M))P.<x> = PolynomialRing(Zmod(p), implementation='NTL')
f = x ^ e - c
res1 = f.monic().roots()P.<x> = PolynomialRing(Zmod(q), implementation='NTL')
f = x ^ e - c
res2 = f.monic().roots()P.<x> = PolynomialRing(Zmod(r),implementation='NTL')
f = x ^ e - c
res3 = f.monic().roots()for i in res1:for j in res2:for k in res3:param1 = [int(i[0]), int(j[0]), int(k[0])]param2 = [p, q, r]m = CRT_list(param1, param2)flag = long_to_bytes(m)if b'flag{' in flag:print(flag)

[WEEK3]Classical Master

重合指数 第一次见
建议看密码爷糖醋小鸡块的博客
https://tangcuxiaojikuai.xyz/post/165cec8c.html#more

web

[week_3]ez_rce(todo)

[WEEK3]gogogo(todo)