已解决
吴恩达《机器学习》2-1:模型描述
来自网友在路上 136836提问 提问时间:2023-10-31 21:16:11阅读次数: 36
最佳答案 问答题库368位专家为你答疑解惑
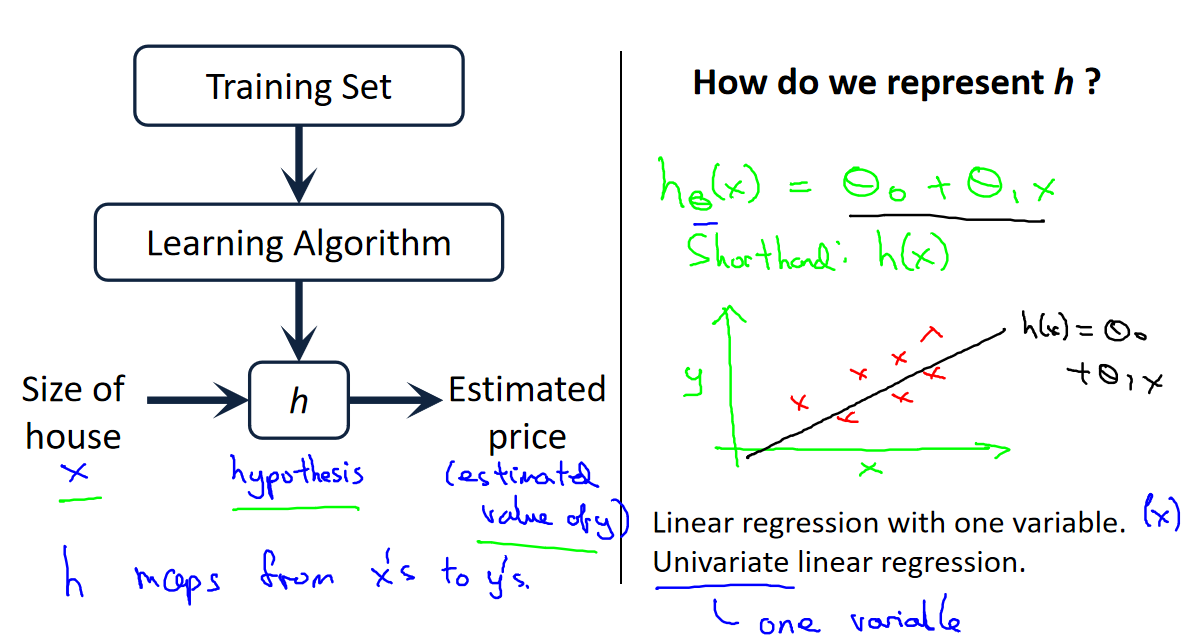
一、单变量线性回归
单变量线性回归是监督学习中的一种算法,通常用于解决回归问题。在单变量线性回归中,我们有一个训练数据集,其中包括一组输入特征(通常表示为𝑥)和相应的输出目标(通常表示为𝑦)。这个算法的目标是学习一个线性函数,通常表示为ℎ𝜃(𝑥),其中𝜃是要学习的参数,以便将输入特征映射到输出目标。
具体地,对于单变量线性回归,通常使用以下形式的线性函数:
其中:
- ℎ𝜃(𝑥) 表示通过算法学习到的假设(或预测)函数。
- 𝜃0 和 𝜃1 是要学习的模型参数,分别表示假设的截距和斜率。
- 𝑥 是输入特征,通常表示单个特征。
- 𝑦 是输出目标,表示要预测的结果。
单变量线性回归的目标是通过训练数据集学习出最佳的模型参数𝜃0和𝜃1,使得假设ℎ𝜃(𝑥)能够最好地拟合训练数据集中的输入特征和输出目标。一旦学习到了合适的参数,就可以使用模型来进行预测,根据给定的输入特征𝑥,预测相应的输出目标𝑦。
在单变量线性回归问题中,我们通常通过最小化成本函数(例如均方误差)来找到最佳的参数𝜃0和𝜃1,以使模型与训练数据尽可能接近。这就是单变量线性回归的基本思想,它可用于估计输入特征与输出目标之间的线性关系,例如根据房屋尺寸来估计房屋价格。
参考资料:
[中英字幕]吴恩达机器学习系列课程
黄海广博士 - 吴恩达机器学习个人笔记
查看全文
99%的人还看了
相似问题
猜你感兴趣
版权申明
本文"吴恩达《机器学习》2-1:模型描述":http://eshow365.cn/6-29016-0.html 内容来自互联网,请自行判断内容的正确性。如有侵权请联系我们,立即删除!
- 上一篇: Redis-双写一致性
- 下一篇: 极智AI | 从大模型角度看苹果M3系列芯片