平衡二叉树

基本介绍

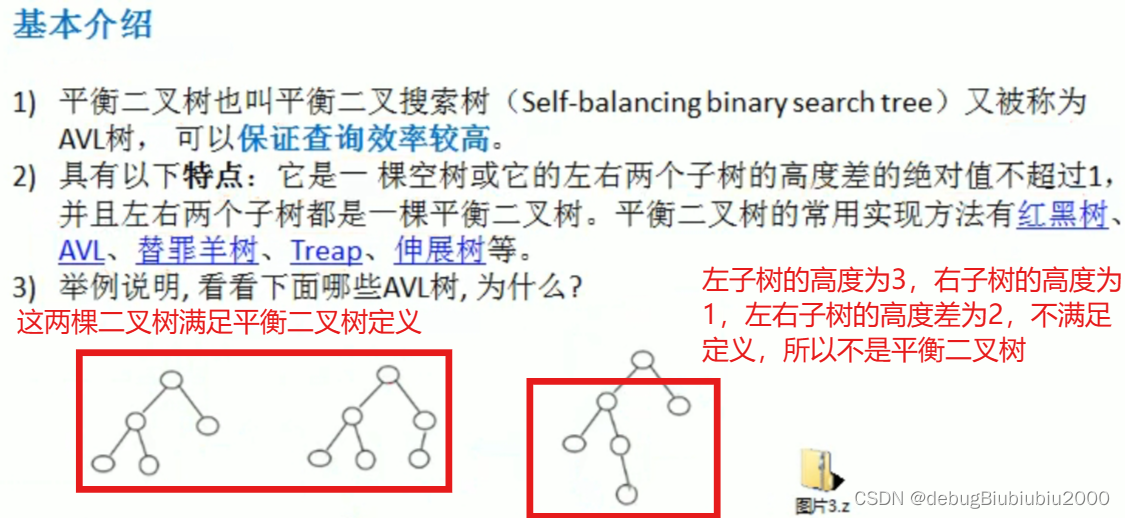
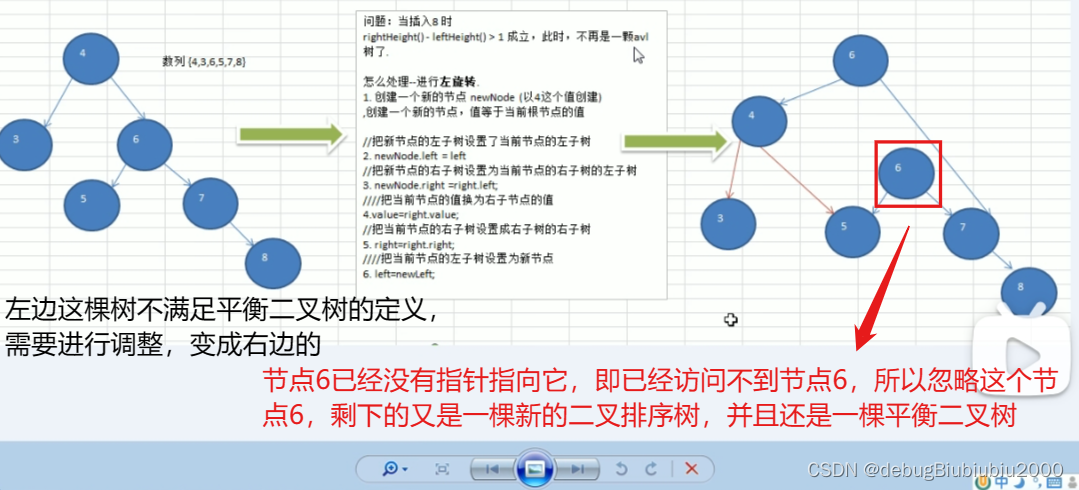
左旋转调整成平衡二叉树

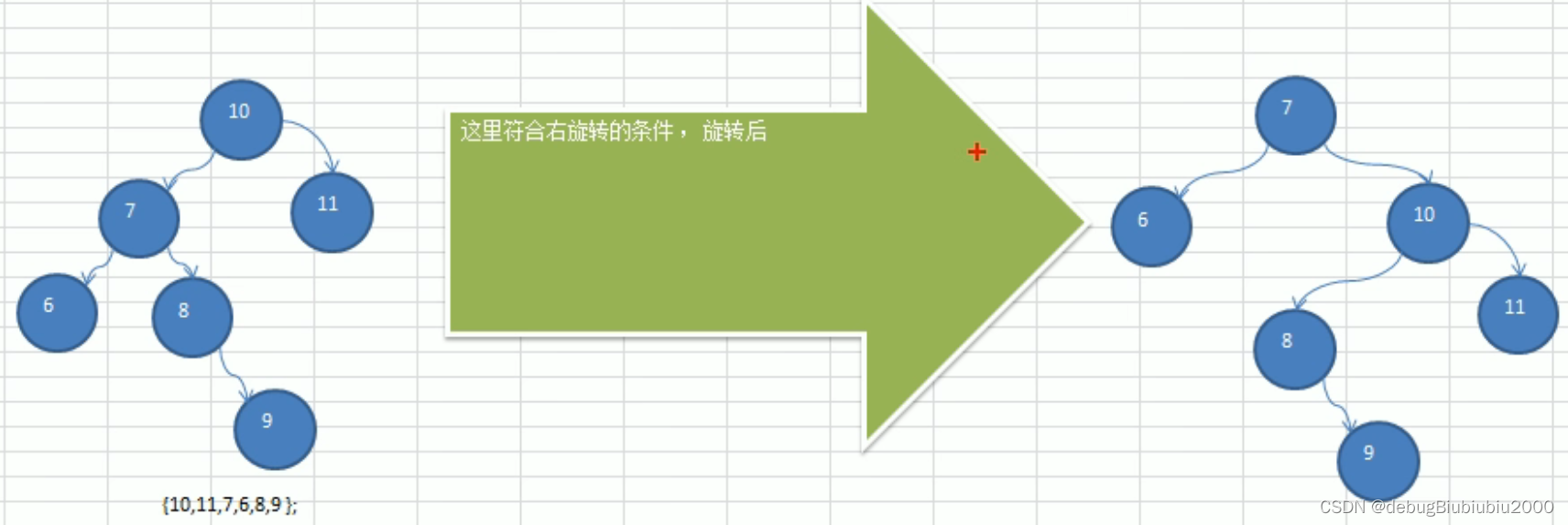
右旋转调整成平衡二叉树

双旋转调整成平衡二叉树

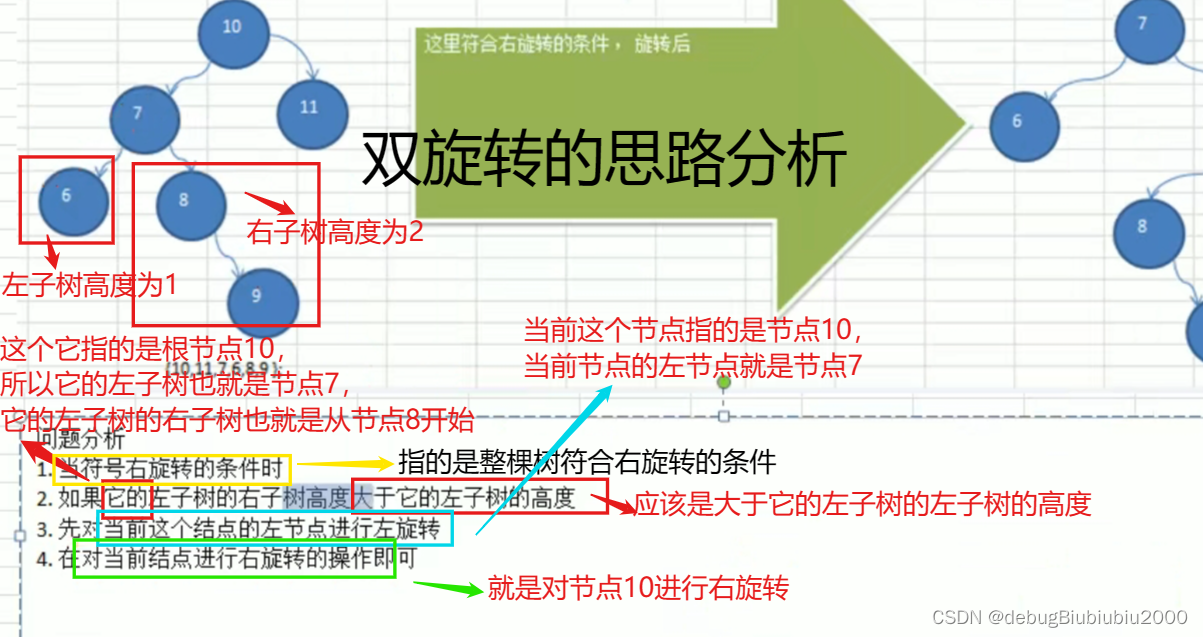
上述三种旋转方式的代码实现

class Node:"""创建 Node 节点"""value: int = 0left = Noneright = Nonedef __init__(self, value: int):self.value = valuedef height(self):"""返回以当前节点为根节点的树的高度"""# 如果左子树不为空，则遍历左子树，最终获得左子树的高度# 如果右子树不为空，则遍历右子树，最终获得右子树的高度# 返回左右子树两个高度中的较大的那个值# 加1是因为当前节点要算一层高度return max(self.left.height() if self.left else 0, self.right.height() if self.right else 0) + 1def left_height(self):"""返回左子树的高度"""if self.left:return self.left.height()return 0def right_height(self):"""返回右子树的高度"""if self.right:return self.right.height()return 0def left_rotate(self):"""通过左旋转的方式调整二叉树为平衡二叉树"""# 以当前节点的值创建一个新的节点new_node = Node(self.value)# 把新节点的左子树设置为当前节点的左子树new_node.left = self.left# 把新节点的右子树设置为当前节点的右子树的左子树new_node.right = self.right.left# 把当前节点的值替换为当前节点右子节点的值self.value = self.right.value# 把当前节点的右子树设置为当前节点右子树的右子树self.right = self.right.right# 把当前节点的左子树设置为新节点self.left = new_nodedef right_rotate(self):"""通过右旋转的方式调整二叉树为平衡二叉树"""# 以当前节点的值创建一个新的节点new_node = Node(self.value)# 把新节点的右子树设置为当前节点的右子树new_node.right = self.right# 把新节点的左子树设置为当前节点的左子树的右子树new_node.left = self.left.right# 把当前节点的值替换为当前节点左子节点的值self.value = self.left.value# 把当前节点的左子树设置为当前节点左子树的左子树self.left = self.left.left# 把当前节点的右子树设置为新节点self.right = new_nodedef add(self, node):"""添加节点node 表示要添加的节点"""if node is None:return# 判断要添加节点和当前子树根节点的大小if node.value < self.value:# 要添加节点小于当前子树根节点if self.left is None:# 如果当前子树左子节点为空，则直接将要添加的节点挂在左子节点上self.left = nodeelse:# 否则，递归当前子树的左节点，找到要放置的位置self.left.add(node)else:  # 要添加节点大于等于当前子树根节点if self.right is None:# 如果当前子树右子节点为空，则直接将要添加的节点挂在右子节点上self.right = nodeelse:# 否则，递归当前子树的右节点，找到要放置的位置self.right.add(node)# 添加完一个节点后，如果 （右子树高度 - 左子树高度） > 1，则进行左旋转# 之所以叫左旋转，是因为右子树的高度高于左子树，需要将右子树调整（个人理解）if self.right_height() - self.left_height() > 1:# 如果当前节点右子树的左子树高度大于当前节点右子树的右子树高度# 则进行双旋转操作（先右旋转再左旋转）if self.right and self.right.left_height() > self.right.height():# 先对当前节点的右节点进行右旋转self.right.right_rotate()# 然后对当前节点进行左旋转self.left_rotate()else:  # 否则，直接左旋转self.left_rotate()# ！！！这里必须节return，否则会继续往下判断，有可能会出错return# 添加完一个节点后，如果 （左子树高度 - 右子树高度） > 1，则进行右旋转# 之所以叫右旋转，是因为左子树的高度高于右子树，需要将左子树调整（个人理解）if self.left_height() - self.right_height() > 1:# 如果当前节点左子树的右子树高度大于当前节点左子树的左子树高度# 则进行双旋转操作（先左旋转再右旋转）if self.left and self.left.right_height() > self.left.left_height():# 先对当前节点的左节点进行左旋转self.left.left_rotate()# 然后对当前节点进行右旋转self.right_rotate()else:  # 否则，直接右旋转self.right_rotate()def infix_order(self):"""中序遍历二叉树"""if self.left:self.left.infix_order()print(self.value, end=' ')if self.right:self.right.infix_order()class AVLTree:"""二叉排序树"""root: Node = Nonedef add(self, node: Node):"""添加节点node: 要添加的节点"""if self.root is None:# 如果根节点为空，直接将新节点当做根节点self.root = nodeelse:# 否则，将新节点放在根节点下self.root.add(node)def infix_order(self):"""中序遍历"""if self.root:self.root.infix_order()print()else:print("二叉排序树为空...")# 测试左旋转
arr = [4, 3, 6, 5, 7, 8]
avl_tree = AVLTree()
for i in arr:node = Node(i)avl_tree.add(node)
avl_tree.infix_order()
print("左旋转处理过后：")
print("树的高度：", avl_tree.root.height())
print("树的左子树高度：", avl_tree.root.left.height())
print("树的右子树高度：", avl_tree.root.right.height())
# 测试右旋转
arr = [10, 12, 8, 9, 7, 6]
avl_tree = AVLTree()
for i in arr:node = Node(i)avl_tree.add(node)
avl_tree.infix_order()
print("右旋转处理过后：")
print("树的高度：", avl_tree.root.height())
print("树的左子树高度：", avl_tree.root.left.height())
print("树的右子树高度：", avl_tree.root.right.height())# 测试双旋转
arr = [10, 11, 7, 6, 8, 9]
avl_tree = AVLTree()
for i in arr:node = Node(i)avl_tree.add(node)
avl_tree.infix_order()
print("双旋转处理过后：")
print("树的高度：", avl_tree.root.height())
print("树的左子树高度：", avl_tree.root.left.height())
print("树的右子树高度：", avl_tree.root.right.height())