ZKP学习笔记

ZK-Learning MOOC课程笔记

Lecture 5: The Plonk SNARK (Dan Boneh)

5.2 Proving properties of committed polynomials

• overview
  

• Polynomial equality testing with KZG

  • KZG: determined commitment (if the function is equal, then the commitment is equal too)

    • If the $co{m}_f=co{m}_g$, the verifier can tell if $f=g$ on its own???

    • but
      

      • The verifier does not have the commitment of $g_1{g}_2{g}_3$

• Important proof gadgets for univariates
  

  • The size k is much smaller than d

• The vanishing polynomial
  

  • Outside the $\Omega$, the polynomial could evaluate an arbitrary value
  • Verifiers can evaluate the vanishing polynomial very fast.

• ZeroTest
  

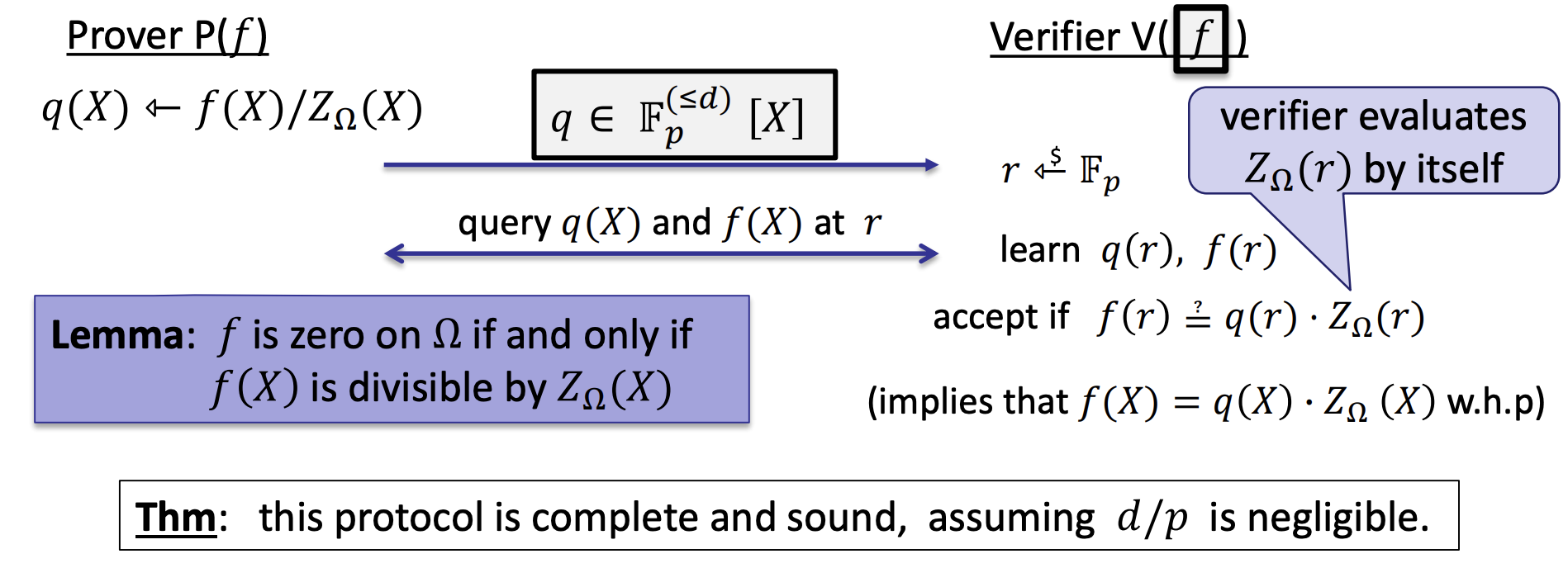
  • F is zero on $\Omega$: All the elements of $\Omega$ are the root of the polynomial.
  • Verifier time: O(log k) and two poly queries (but can be done in one batch)
  • Prover time: dominated by the time to compute q(X) and then commit to q(X)

• Product check
  

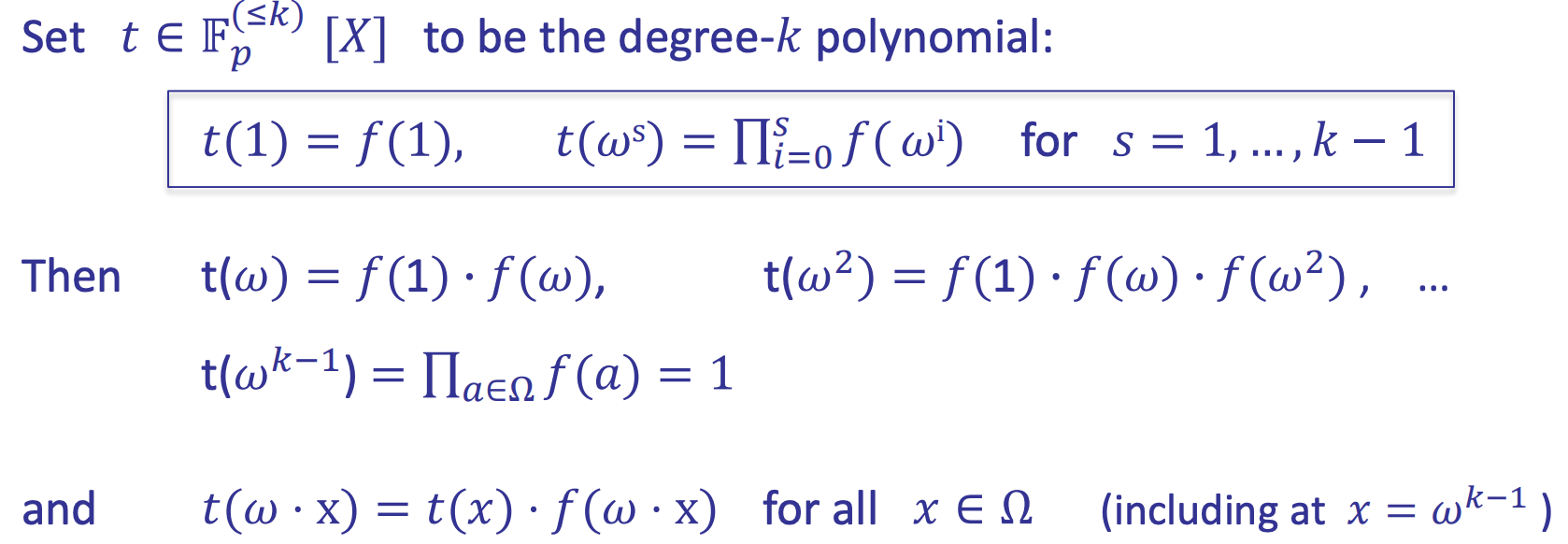
  • Polynomial t: auxiliary polynomial
    

- Use the ZeroTest
- Proof size: two commits, five evals (can be batched). 
- Verifier time: O(logk) 
- Prover time:O(klogk)

• For rational functions
  

• Permutation check
  

• $\hat{f}$ and $\hat{g}$ is identical
• Embellished permutation check
  • The two vectors are permutations to each other
  • They also satisfy a prediscribed pumutation
    

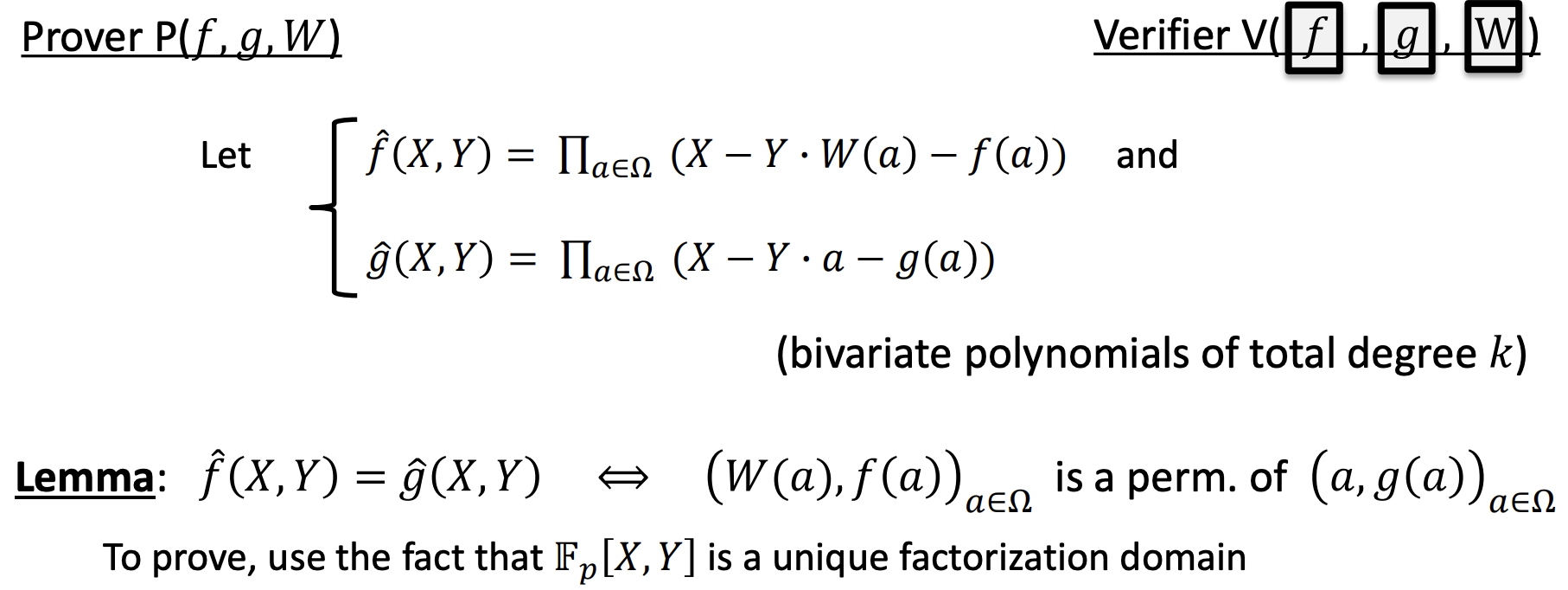
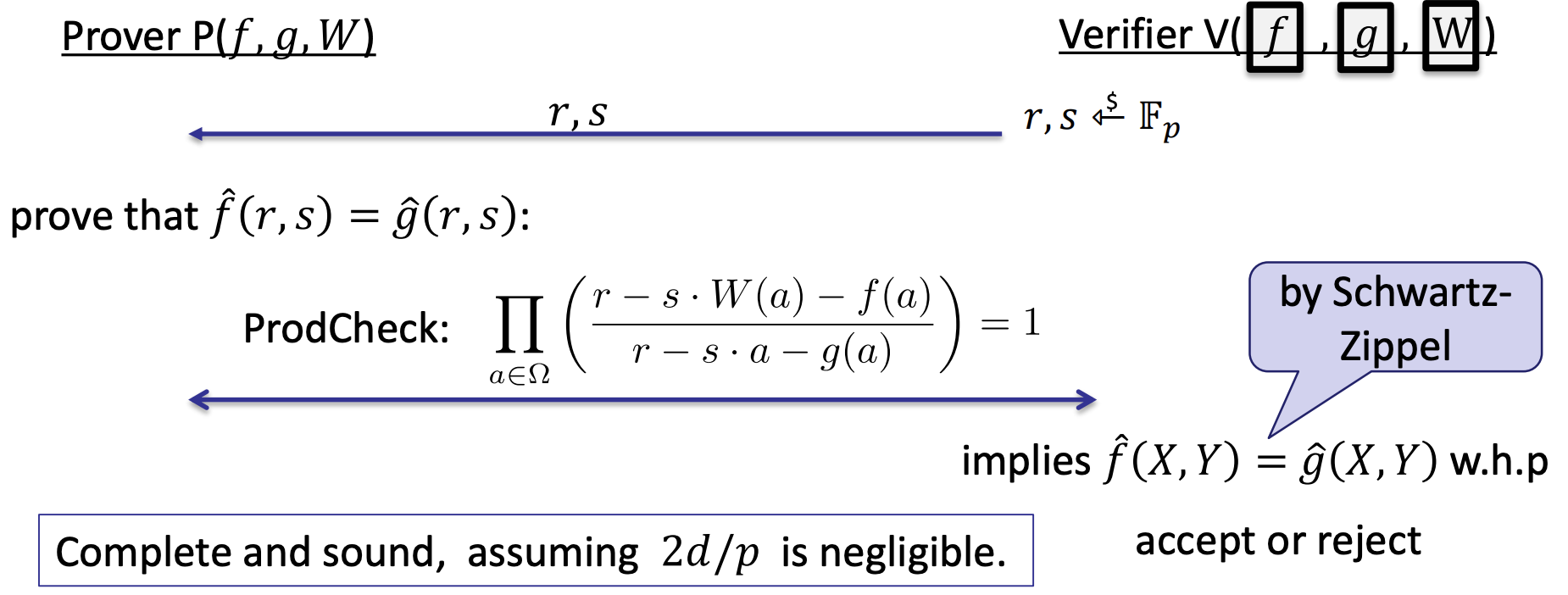
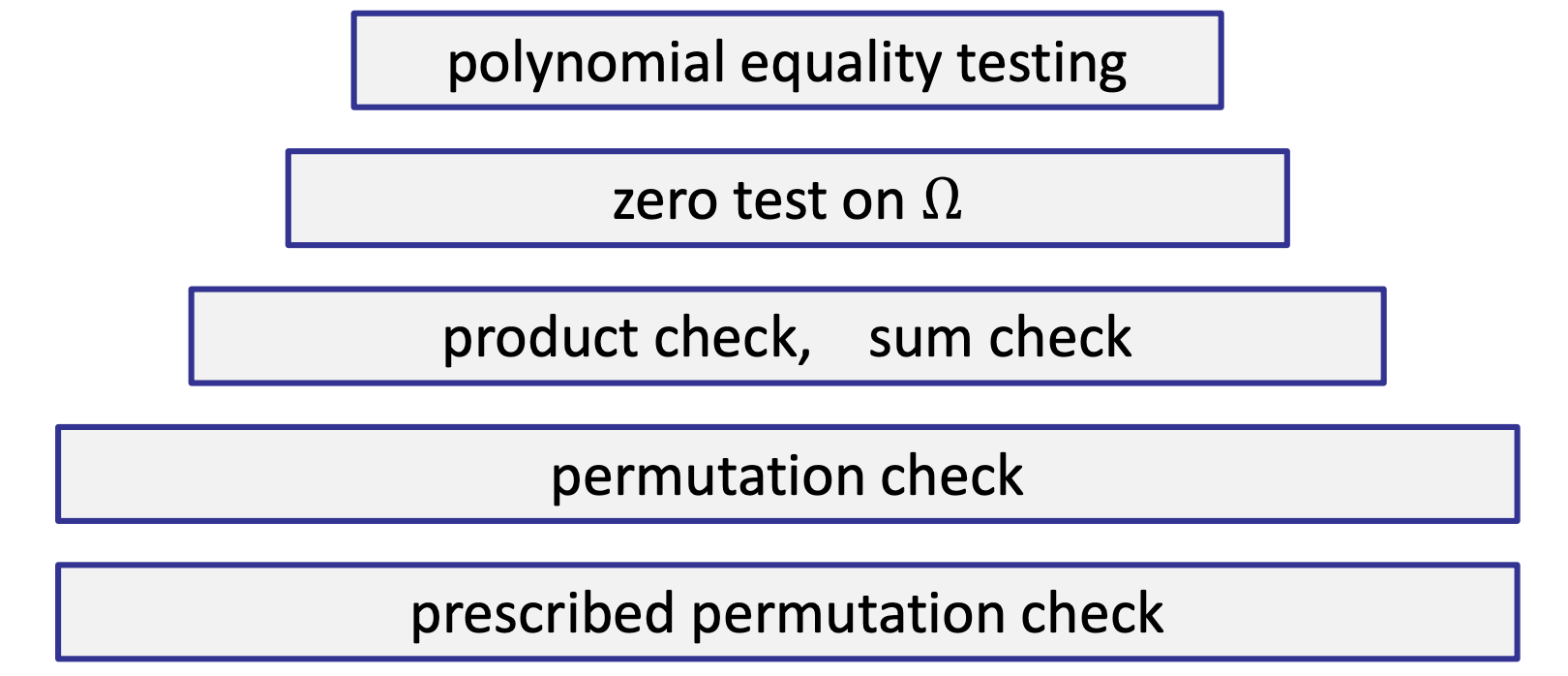
• Summary of proof gadgets
  

5.3 The PLONK IOP for general circuits

• PLONK widely used in practice
  

• PLONK: a poly-IOP for a general circuit
  

  • Encoding the trace as a polynomial
    

• Step 2: proving validity of T
  

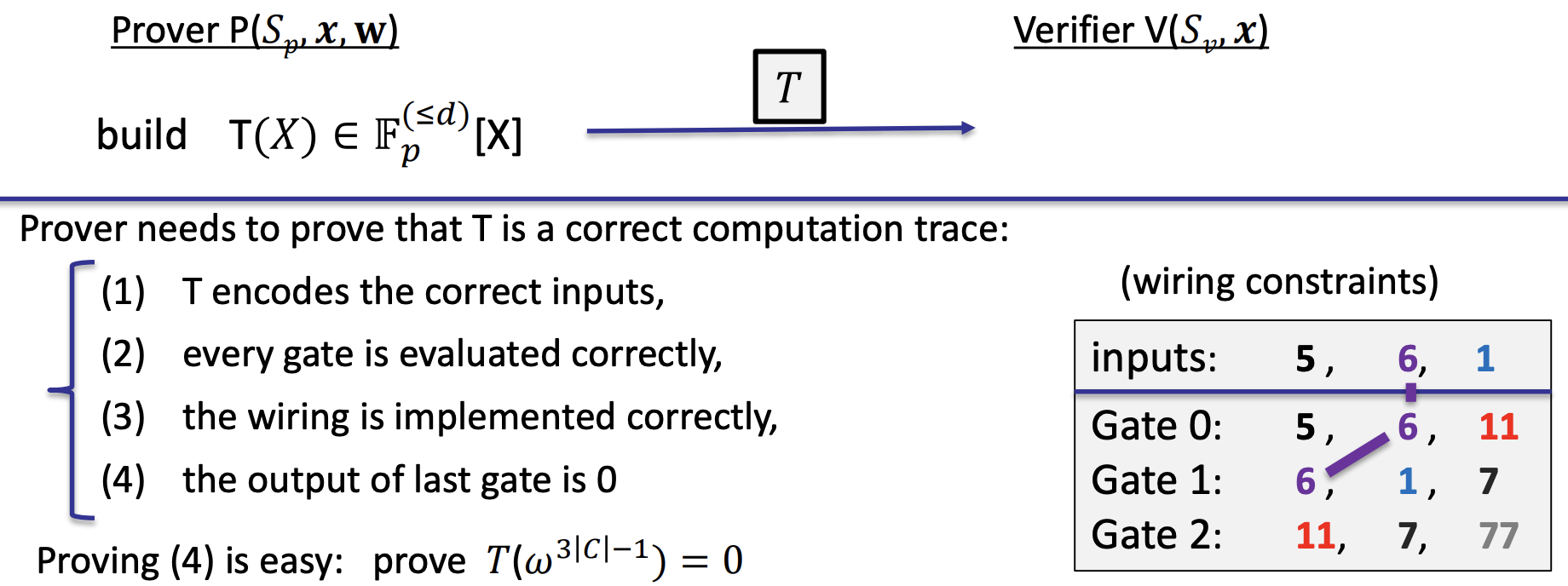
  • (4): the output of the last gate is what the verifier is expecting
  • Proving (1): T encodes the correct inputs
    

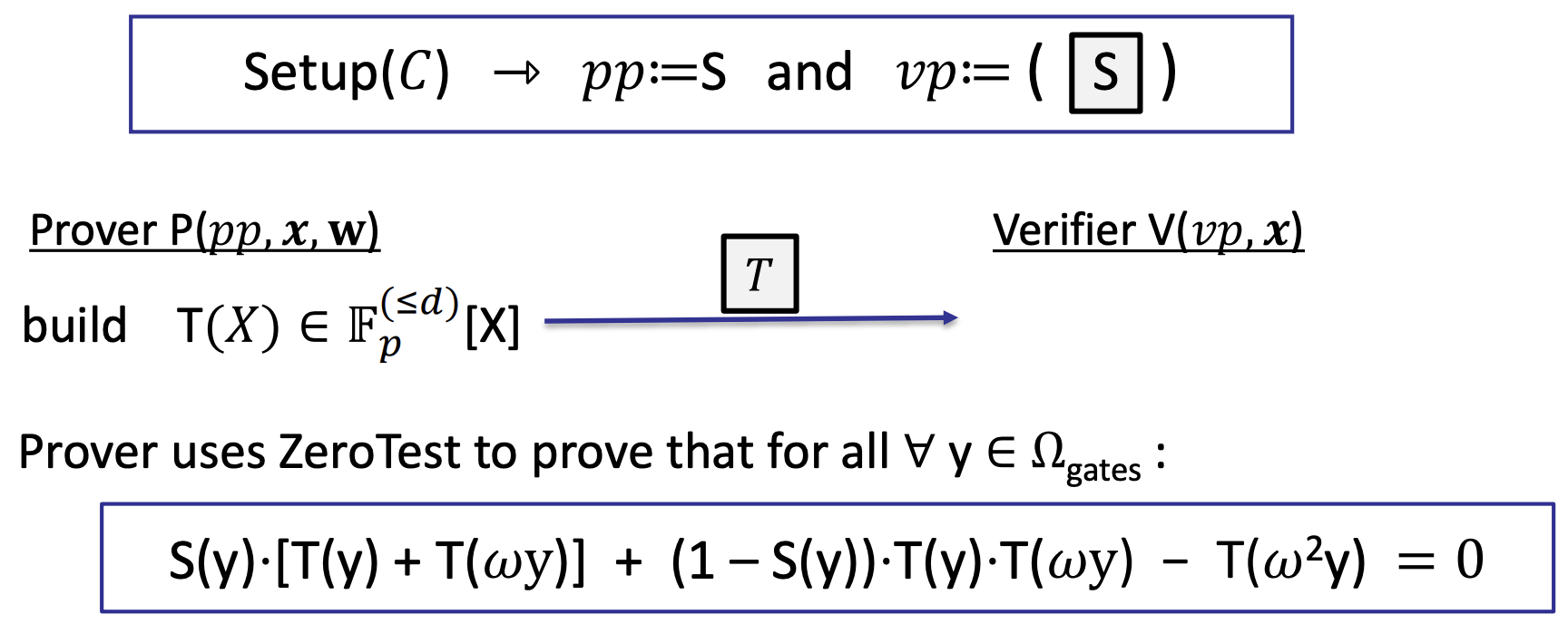
- Proving (2): every gate is evaluated correctly

  - S(X) is a selector- Pre-processing: create the commitment of S(X), it is independent to any input.

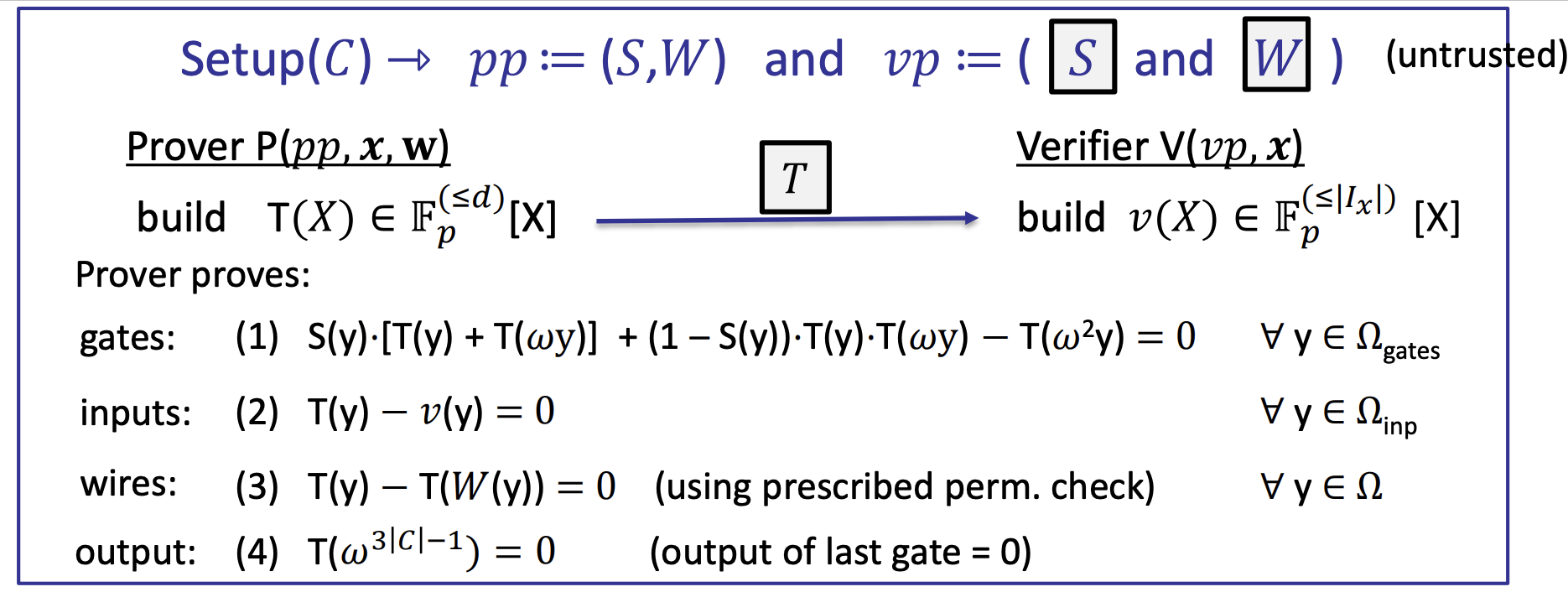
- Proving (3): the wiring is correct

  - The W is independent of the inputs- Prescribed pumutation check

• The complete Plonk Poly-IOP (and SNARK)
  

• Many extensions

  • The SNARK can easily be made into a zk-SNARK

  • Main challenge: reduce prover time
    

  • A generalization: plonkish arithmetization

    • Plonk for circuits with gates other than + and × on rows (custom gates)
      

    • More columns on the table