已解决
leetCode 376.摆动序列 动态规划 + 图解 + 状态转移
来自网友在路上 171871提问 提问时间:2023-10-01 23:52:41阅读次数: 71
最佳答案 问答题库718位专家为你答疑解惑
376. 摆动序列 - 力扣(LeetCode)
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
-
例如,
[1, 7, 4, 9, 2, 5]是一个 摆动序列 ,因为差值(6, -3, 5, -7, 3)是正负交替出现的。 - 相反,
[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
示例 1:
输入:nums = [1,7,4,9,2,5] 输出:6 解释:整个序列均为摆动序列,各元素之间的差值为 (6, -3, 5, -7, 3) 。
示例 2:
输入:nums = [1,17,5,10,13,15,10,5,16,8] 输出:7 解释:这个序列包含几个长度为 7 摆动序列。 其中一个是 [1, 17, 10, 13, 10, 16, 8] ,各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。
示例 3:
输入:nums = [1,2,3,4,5,6,7,8,9] 输出:2
>>思路和分析
官方题解376. 摆动序列 - 力扣(LeetCode)和 这篇文章376. 摆动序列 - 力扣(LeetCode)
给的题解的思路总结和归纳
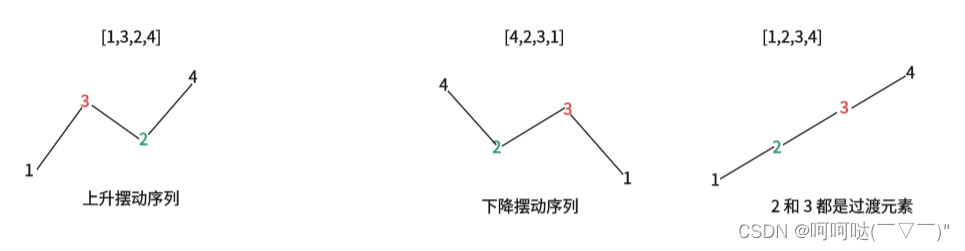
- 序列中的某个元素被称为“峰”,当且仅当该元素两侧的相邻元素均小于它。例如序列[1,3,2,4]中的 3 就是一个“峰”
- 序列中的某个元素被称为“谷”,当且仅当该元素两侧的相邻元素均大于它。例如序列[1,3,2,4]中的 2 就是一个“谷”
- 特别地,对于位于序列两端的元素,只有一侧的相邻元素小于或大于它,也称其为“峰”或“谷”。如序列[1,3,2,4]中,1 也是一个“谷”,4 是一个“峰”
状态定义:
- up[i]:数组 nums[0...i] 中的最长上升摆动序列
- down[i]: 数组 nums[0...i] 中的最长下降摆动序列
状态转移:
- nums[i] > nums[i-1]: up[i] = down[i-1] + 1; down[i] = down[i-1]
- nums[i] < nums[i-1]: up[i] = up[i-1]; down[i] = up[i-1] + 1


class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int n = nums.size();if (n < 2) {return n;}int up = 1, down = 1;for (int i = 1; i < n; i++) {if (nums[i] > nums[i - 1]) {up = down + 1;} else if (nums[i] < nums[i - 1]) {down = up + 1;}}return max(up, down);}
};// 作者:力扣官方题解
// 链接:https://leetcode.cn/problems/wiggle-subsequence/solutions/805292/python3-yi-tu-sheng-qian-yan-by-v12de-ao-72b1/
// 来源:力扣(LeetCode)
// 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。我的往期文章:leetCode 376.摆动序列 贪心算法_呵呵哒( ̄▽ ̄)"的博客-CSDN博客
推荐文章:
376. 摆动序列 - 力扣(LeetCode)
376. 摆动序列 - 力扣(LeetCode)
查看全文
99%的人还看了
相似问题
- 【Django-DRF用法】多年积累md笔记,第3篇:Django-DRF的序列化和反序列化详解
- 【Java 进阶篇】JavaScript JSON 语法入门:轻松理解数据的序列化和反序列化
- 【python学习】基础篇-常用模块-pickle模块:序列化和反序列化
- ZC序列理论学习及仿真
- 时间序列预测实战(十七)PyTorch实现LSTM-GRU模型长期预测并可视化结果(附代码+数据集+详细讲解)
- 代码随想录算法训练营第二十九天| 491 递增子序列 46 全排列
- 最长递增子序列
- 深入解析序列模型:全面阐释 RNN、LSTM 与 Seq2Seq 的秘密
- c#Nettonsoft.net库常用的方法json序列化反序列化
- 基于C#实现最长公共子序列
猜你感兴趣
版权申明
本文"leetCode 376.摆动序列 动态规划 + 图解 + 状态转移":http://eshow365.cn/6-15586-0.html 内容来自互联网,请自行判断内容的正确性。如有侵权请联系我们,立即删除!
- 上一篇: Codeforces Round 899 (Div. 2)
- 下一篇: opencv图像数组坐标系