4406. 积木画 - AcWing题库 

题目描述

分析

 在完成此问题前可以先引入一个新的问题

291. 蒙德里安的梦想 - AcWing题库

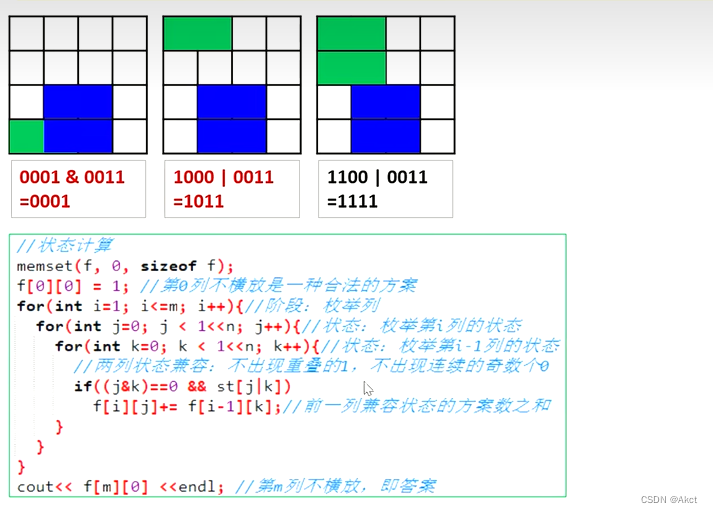
我们发现16的二进制是 10000

15的二进制是1111

故刚好我们可以从0枚举到1 << n(相当于二的n次方的二进制表示）

注：奇数个0是非法的 

此处i的变化记录的是每一个状态，

这里的i每次>>j 是来记录i这个状态中0和1的个数，如果在这个过程中i是1就要看前面记录的0的个数，如果0的个数是奇数，那就会是1101这种类似状态故一定不符合事实

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 12, M = 1 << N;
ll n, m, f[N][M];
bool st[N];
int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);while(cin >> n >> m){if(n == 0 && m == 0)break;for(int i = 0; i < 1 << n; i ++){st[i] = true;int cnt = 0;for(int j = 0; j < n; j ++){if(i >> j & 1){if(cnt & 1){st[i] = false;break;}}else cnt ++;}if(cnt & 1)st[i] = false;//eg.0100}memset(f, 0, sizeof f);f[0][0] = 1;for(int i = 1; i <= m; i ++){for(int j = 0; j < 1 << n; j ++){for(int k = 0; k < 1 << n; k ++){if((j & k) == 0 && st[j | k]){f[i][j] += f[i - 1][k];}}} }cout << f[m][0] << '\n';}return 0;
}

题目分析

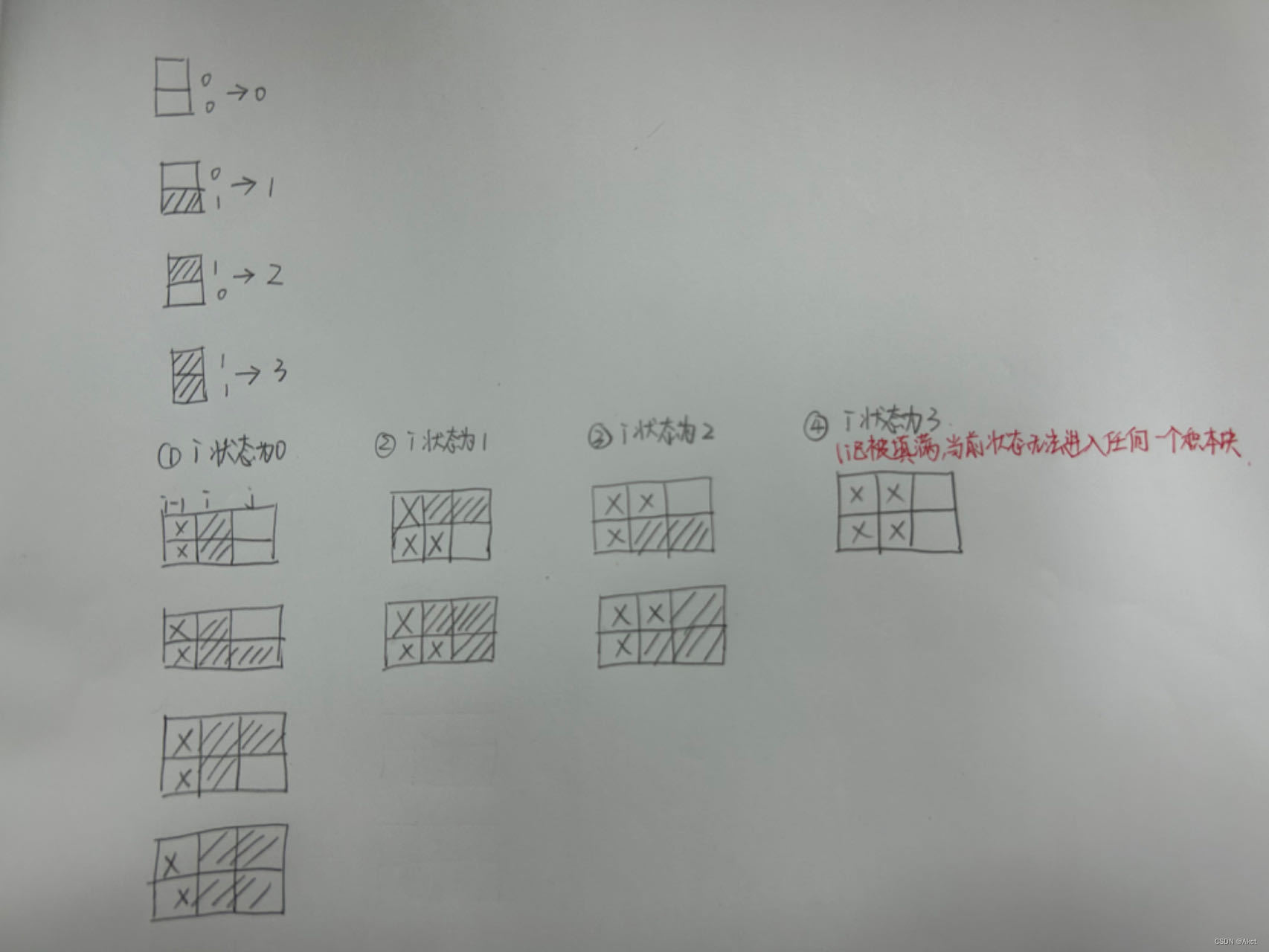
发现一共有16种转移状态

DP[i][j]表示已经操作完i - 1列且第i列的状态为j的所有方案的集合

#include<bits/stdc++.h>
using namespace std;
const int N = 1e7 + 10;
const int mod = 1000000007;int g[4][4] = 
{{1, 1, 1, 1},{0, 0, 1, 1},{0, 1, 0, 1},{1, 0, 0, 0}, 	
};
int dp[N][4];
int main()
{int n;cin >> n;dp[1][0] = 1;for(int i = 1; i <= n; i ++)//枚举列数 {for(int j = 0; j < 4; j ++)//从j状态转移到k状态 {for(int k = 0; k < 4; k ++)//表示向k状态转移 {dp[i + 1][k] = (dp[i + 1][k] + g[j][k] * dp[i][j]) % mod;}}}cout << dp[n + 1][0];return 0;
}

列举此位置的所有状态(j)每次乘上可以转化为的所有状态(k),然后不断将此位置的所有状态相加得到此位置的所有状态，最后输出最后一列(n)且下一列所有状态为0，也就是没有伸出的一列