整理低秩的理解
最佳答案 问答题库488位专家为你答疑解惑
秩的定义是矩阵中非零特征值的个数。比如一个NxN的矩阵,它的秩为r,r远小于N,我们可以说它是低秩的。
但还有另一种情况:这个矩阵的的秩接近N,但它的特征值大多数接近于0,只有少数几个特征值特别大,这种也可以认为是低秩的。如果我们将低秩图像的特征值从大到小排列,会得到这样一条曲线:
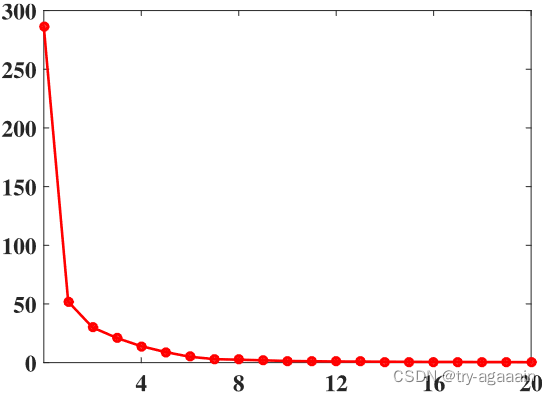
(纵坐标为特征值的大小,横坐标为不同的特征值下标)
可以从特征向量的角度来理解低秩的含义:矩阵只需要极少数的几个特征向量就能近似还原出原先矩阵中的每个向量。
在用这些特征向量还原矩阵的过程中,这些特征向量起到的作用是有差异的,特征值越大的特征向量,它和矩阵中的大部分向量越相似,所以只需要用前几个重要特征向量进行线性组合,就能近似的还原矩阵中的大多数向量。
如果我们将低秩矩阵X分解为A*Z,可以将A看作是特征向量,或者说是基向量组(基底),Z为图像的系数表示矩阵。那么可以取前r个特征向量 A ′ = A ∈ R N × r A'=A \in R^{N \times r} A′=A∈RN×r和对应的系数矩阵 Z ′ = Z ∈ R r × N Z'=Z \in R^{r \times N} Z′=Z∈Rr×N相乘,得到 X ′ = A ′ ∗ Z ′ X'=A'*Z' X′=A′∗Z′的和原矩阵X是很接近的。
下面选用了一张有较多重复图案的图像,这类图像由于图像细节的相似性往往具有低秩特点,在RGB三通道上进行依次选用前k个特征向量来还原原图:

可以看到,仅使用一个特征向量便能大致刻画图像的图案特征,当选用前20个特征向量时,基本能很好的还原出原始图像的细节了。
在刚接触PCA时,常将其用于数据压缩,比如一个多分类问题,每条样本包含大量的属性,而有些属性并不关键,去掉这些属性对分类影响不大,于是通过PCA将原先由N个属性表示的样本压缩为r(r<<N)个属性表示,使数据的处理更加方便。在这个过程中,剩下的信息也是用少数r个特征向量来表示的,它们对应的特征值都较大。
我们会用能量来表示特征向量的作用,它计算很简单,第i个特征向量的能量为:该特征值 / 所有特征值之和。对于低秩矩阵来说,用能量占90%以上的前几个特征就能表示出原矩阵了,恢复的误差很小。即使是一般的图像,也常常会用类似的方式进行压缩,在图像的传输中,为节省流量往往进行压缩,我们有时候会看到一些高糊的表情包,可能就是不断压缩的结果(趣称为“电子包浆”)。
99%的人还看了
相似问题
- 23. 深度学习 - 多维向量自动求导
- 【腾讯云云上实验室-向量数据库】探索腾讯云向量数据库:全方位管理与高效利用多维向量数据的引领者
- 分类预测 | Matlab实现基于DBN-SVM深度置信网络-支持向量机的数据分类预测
- 【VRTK】【VR开发】【Unity】7-配置交互能力和向量追踪
- 【腾讯云云上实验室-向量数据库】TAI时代的数据枢纽-向量数据库 VectorDB
- 计算两个向量的叉积numpy.cross()
- LangChain 4用向量数据库Faiss存储,读取YouTube的视频文本搜索Indexes for information retrieve
- 《向量数据库指南》——什么是 向量数据库Milvus Cloud的Range Search?
- 《向量数据库指南》——亚马逊云科技向量数据库揭秘:点亮数据未来!
- 亚马逊云Amazon OpenSearch Serverless“利刃在手,‘向量’八方“
猜你感兴趣
版权申明
本文"整理低秩的理解":http://eshow365.cn/6-39329-0.html 内容来自互联网,请自行判断内容的正确性。如有侵权请联系我们,立即删除!
- 上一篇: Egress-TLS-Origination
- 下一篇: DRF统一返回格式